ジオメトリ:ポリゴン

凸および凹ポリゴン

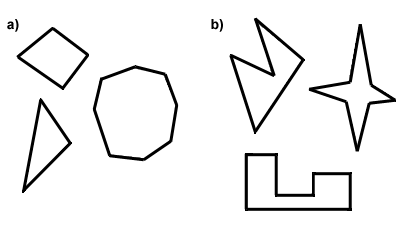
すべてのポリゴンは凸または凹のいずれかです。 凸多角形と凹多角形の間の違いは、それらの角度の尺度にある。 多角形が凸になるためには、その内角はすべて180度未満でなければなりません。 それ以外の場合は、ポリゴンは それを考える別の方法はこれです：convexpolygonの対角線はすべてポリゴンの内部にありますが、凹ポリゴンの特定の対角線はポリゴンの外側にあります。, Below in Part A are some convex polygons, and in Part B, some concave polygons. In the rest of this text, you can assume that every polygon discussed is convex.

Regular Polygons

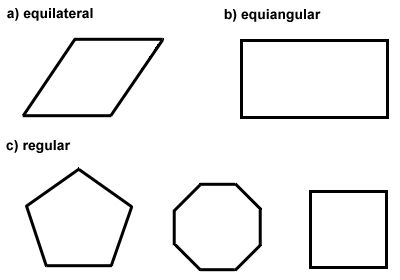
Polygons can also be classified as equilateral, equiangular, or both. Equilateral polygons have congruent sides, like a rhombus. Equiangular polygons have congruent interior angles, like a rectangle., 多角形が正三角形と等角三角形の両方である場合、それは正多角形と呼ばれます。 正方形は正多角形の一例です。 正多角形の中心は、多角形のすべての頂点が等距離にある点です。 正多角形には、次のセクションで説明する特別なプロパティがあります。 以下に、等角多角形、等辺多角形、正多角形の例を示します。,

Congruent Polygons

One more note on polygons: Polygons whose sides are all congruent are congruent polygons. Knowing this term will be important later. In congruent polygons, every segment is congruent.