今日は、最も人気のあるオプションの価格モデルを見てみましょう。 ブラック-ショールズ-モデル（Black-Scholes-Merton method）は、価格オプション契約の数学的モデルである。 これは、金融商品の変動を推定することによって機能します。 この手法は、価格が対数正規分布に従うという仮定に依存しています。 これに基づいて、オプションの値を導出します。,

これは、投資家が期日までに行使することができないパス非依存オプションに適しています。 これは、パス依存オプション（例えば、アメリカのオプション）を評価するためのリスク中立的な方法である二項オプション価格モデルとは異なります。

アナリストや投資家は、ブラック-ショールズは現代の金融理論における本質的な概念の一つであると考えています。

1973年にFischer BlackとMyron ScholesによってJournal of Political Economyに導入され、後にRobert Mertonによって構築され、このモデルは1997年にノーベル経済学賞を受賞しました。,

このモデルは、オプションの価格を解くために使用する微分方程式に従います。 私達はヨーロッパ式の選択のためにモデルの標準的な変化を使用する。 Black Scholesは、投資家が有効期限の前にいつでもこれらのオプションを行使できるとは考えていないため、アメリカンスタイルのオプションには適して

この方法では、原資産の価格が負になることはできないため、対数正規分布に従うと想定しています。 このモデルが依存する分布は、自然発生するランダムな現象を予測するための理論であるブラウン運動に基づいています。,

このモデルを使用して、オプションの価格の見積もりを計算します。

  • 現在の価格、
  • 行使価格、
  • 有効期限、
  • 期待配当利回り、
  • 期待金利、および
  • 期待ボラティリティ。
  • オプションのオプション価格の見積もりを計算します。
    • オプション価格の見積もりを計算します。
      • オプション価格の見積もりを計算します。

      当初、このモデルでは配当支払いの影響は考慮されていません。 したがって、それは頻繁に原資産の配当落ち日の値を決定することによってそうするように適応しています。, 配当利回りは、オプションホルダーが配当を忘れるため、現在の株価を下げる効果があります。

      仮定

      ブラック-ショールズ-モデルは、特定の仮定をした場合にのみ機能します。,つまり、市場は完全に効率的であり、動きを予測することはできません。

    • 売買オプションは取引コストを伴わない。
    • 原資産のボラティリティとリスクフリーレートの両方が有効期限まで一定であり、実際には需要と供給によってボラティリティがシフトするため、正しくない。
    • 原資産のリターンは、原資産のボラティリティとリスクフリーレートの両方が満了日まで一定である。正規分布に従います。,

    Black Scholes Formula

    モデル式は数学的に非常に複雑ですが、特殊なツールを使用して計算できるため、これは特に問題ではありません。 いますが、残念ながら不可欠なろう”と思われたはずです。,

    コールオプションの価格を計算するには、Black Scholesモデルの下で、次の式を使用できます。

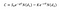
    ここで、

    • s0は株価です。
    • eは指数数です。
    • qは配当利回りの割合です。
    • tは用語です（一年はt=1、半年はt=0になります。,5);
    • N(d1)はコールオプションのデルタであり、株価のシフトに対するコール価格の変化を意味します。
    • Kは行使価格です。
    • rはリスクフリーレートです。
    • N(d2)は、将来の株価が行使価格よりも高くなる確率であり、オプションを行使する可能性です。

    一方の側は、d1の累積標準正規分布を掛けた株価であり、他方の行使価格は、時間Tに割引され、d2の累積標準正規分布を掛けたものです。,

    ここで、d1とd2を次の式で計算できます。

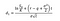
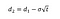
    ここで、θは原資産のリターンのボラティリティです。,

    プットオプションにも同じロジックを適用できます。

    無料のexcelベンチマーク分析テンプレートのための私たちのニュースレターに参加

    ブラック-ショールズ計算の例

    ブラック-ショールズ-モデルの背後にある概念をよりよく説明するために、次のモデルを見てみましょう。 まず、モデル入力から始めます。, 上記のように、コールとプットオプションの値を計算するには、次の六つの変数が必要です。

    次に、オプションのパラメータを計算します。 D1から始めると、モデルの仮定から0.39が得られます。

    それを計算するには、d1の式をExcelに転送するだけです。,

    Following the same approach, we calculate d2, N(d1) and N(d2).

    With those, we can calculate the Call Option Price and the Put Option Price.,

    コールプットパリティルールを使用して、数式と計算が正しいかどうかを確認できます—–

    現在、この会社のモデルを計算し、コール、プット-オプション価格 性能を持っておりますが、さらに一歩進み、どのように異なる入力パラメータの影響は、結果のモデルです。, Excelのデータテーブル機能は、変数の感度分析テーブルを準備するのに最適なツールです。 データテーブルの使用方法については、感度分析の記事を参照してください。

    それは€10から€100に変更された場合のは、株価を見てみましょうし、それがコールとプット値にどのように影響します。 株価が€40に達するまで、コールオプションには値がないことがわかります。 私たちは、株価が€85を上回ると、その値がゼロに当たるプットオプションの逆を参照してください。,

    行使価格に対して同じ感度テーブルを準備する場合、逆の関係を観察することができます。 行使価格が上昇するにつれて、コール値が下がり、プット値が上がります。

    また、リスクフリーレートを見てみましょう—–, それが増加すると、これはまた、リターンの必要な率を増加させます。 その後、これは株式の価値を低下させる。 プットオプション値は、その価値を減少させながら、我々は、リスクフリーレートが増加するにつれて、コールオプション値は、同様に増加し、直接的な関係に気づ

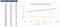
    同じアプローチに従うと、先に行くと見ることができます残りのパラメータとそれらがオプション値にどのように影響するか, 記事の最後にExcelモデルをダウンロードし、そこで感度分析を行うことができます。

    元の記事でExcelでモデル例をダウンロードできます。

    結論

    Black-Scholes-Mertonモデルは理論的な概念であることを覚えておくことが重要です。 私たちは、市場の行動を試してみて、推定するためにそれを使用します。 しかし、意思決定プロセスで結果を使用する場合、モデルの根底にある仮定と、それが現実からどのように逸脱しているかを理解する必要があります。,

    式は、それがギャンブルのように見えるように、より人気になるためにオプション取引を助けました。 今日では、様々な修飾黒ショールズに幅広く人気としての基本的な戦略、リスク管理に伴うボラティリティ

    あなたは同僚や友人と記事を共有することで、あなたのサポートを示すことができます。