二つのサイコロを転がす確率

六つのサイコロを転がす確率各ダイの1、2、3、4、5、6ドット。

二つのサイコロが同時にスローされると、イベントの数は62=36になります。 次に、可能な結果を以下の表に示します。,

確率–二つのサイコロのためのサンプルスペース（結果）：

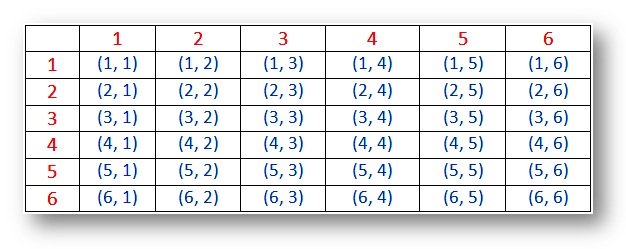
注：

（i）結果(1, 1), (2, 2), (3, 3), (4, 4), (5, 5) そして(6,6)は二重項と呼ばれます。

（ii）ペア（1、2）と（2、1）は異なる結果です。

二つのサイコロを転がすための確率を含むワークアウト問題：

1. 二つのサイコロを巻いています。 A、B、Cをそれぞれ2の合計、3の合計、4の合計を得るイベントとします。, 次に、ことを示す

（i）aは単純なイベントです

（ii）BとCは複合イベントです

（iii）AとBは相互に排他的です

ソリューション：

明らかに、我々は持っています
A={（1、1）}、B= {(1, 2), (2, 1)} およびC= {(1, 3), (3, 1), (2, 2)}.

(i)aは単一のサンプル点で構成されているため、単純なイベントです。

(ii)BとCの両方に複数のサンプル点が含まれているため、それぞれが複合イベントです。

（iii）A≤B=∞であるため、AとBは相互に排他的である。

2. 二つのサイコロを巻いています。, Aは二つのサイコロに示されている数字の合計が5であるイベントであり、Bはサイコロの少なくとも一方が3を示すイベントです。
二つのイベントは、(i)相互に排他的であり、(ii)網羅的ですか？ あなたの答えを支持する引数を与えます。

解決策：

二つのサイコロが転がされると、n（S）があります) = (6 × 6) = 36.

さて、= {(1, 4), (2, 3), (4, 1), (3, 2)}, そして

B= {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}i)A≠B= {(2, 3), (3, 2)} ≠ ∅.

したがって、AとBは相互に排他的ではありません。,

したがって、AとBは網羅的なイベントではありません。

（ii）また、A≤B≤Sです。

したがって、AとB

二つのサイコロを投げるための確率に関する質問に関連するより多くの例。

3. 二つのサイコロがスローされた。, ダブレットの取得

(v)8の合計を取得

(vi)5で割り切れる合計を取得

(vii)少なくとも11の合計を取得

(viii)合計として3の倍数を取得

(ix)少なくとも10の合計を取得

(x)合計として偶数を取得

(x)合計として偶数を取得

(x)合計として偶数を取得

(x)

(xi)和として素数を得る

(xii)偶数のダブレットを得る

(xiii)一方のダイに2の倍数を得ると他方のダイに3の倍数を得る

解決策：

二つの異なるサイコロが同時に投げられ、1、2、3、4、5、6の数字が顔に投げられる。, 私たちは、二つの異なるサイコロの単一のスローで、可能な結果の総数は（6×6）=36であることを知っています。

（i）製品として六つを取得する：

E1=製品として六つを取得するイベントをしましょう。 プロダクトが六である数はE1==4

したがって、”製品として六つ”を得る確率

有利な結果の数
P(E1)=可能な結果の総数
=4/36
=1/9

(ii)sum≤3を得る：

E2=sum≤3を得るイベントとする。, 合計≤3がE2==3になる数

したがって、確率’sum≤3’を得る

有利な結果の数
P(E2)=可能な結果の総数
=3/36
=1/12

(iii)sum≤10を得る：

E3=sum≤10を得るイベントとする。 合計≥10の数はE3=

=33

したがって、確率’sum≥10′

有利な結果の数
P(E3)=可能な結果の総数
=33/36
=11/12
(iv)ダブレットを取得する：E4=ダブレットを取得するイベント。, ダブレットがE4==6になる数

したがって、”ダブレット”を得る確率

有利な結果の数
P(E4)=可能な結果の総数
=6/36
=1/6

(v)8の合計を得る：

E5=8の合計を得るイベント。 8の合計である数はE5==5

したがって、確率ofgetting’8の合計’

有利な結果の数
P(E5)=可能な結果の総数
=5/36

(vi)5で割り切れる合計を得る:

E6=5で割り切れる合計を得るイベント。, 5で割り切れる数はE6==7

したがって、”5で割り切れる合計”を得る確率

有利な結果の数
P(E6)=可能な結果の総数
=7/36

(vii)少なくとも11の合計を得る：

E7=少なくとも11の合計を得るイベント。 少なくとも11の合計のイベントはE7==3になります

したがって、確率ofgetting’少なくとも11の合計’

有利な結果の数
P(E7)=可能な結果の総数
=3/36
=1/12

(viii)合計として3のお守りを得る：

E8=合計として3の倍数を得るイベント。, 合計として3の倍数のイベントはE8==12

したがって、”合計として3の倍数”を得る確率

有利な結果の数
P(E8)=可能な結果の総数
=12/36
=1/3

(ix)少なくとも10の合計を得る：

E9=少なくとも10の合計を得るイベント。, 少なくとも10の合計のイベントはE9==6になります

したがって、確率ofgetting’少なくとも10の合計’

好ましい結果の数
P(E9)=可能な結果の総数
=6/36
=1/6

(x)合計としてevennumberを得る：

E10=合計として偶数を得るイベント。, 和として偶数のイベントはE10==18

したがって、確率ofgetting’和として偶数

有利な結果の数
P(E10)=可能な結果の総数
=18/36
=1/2

(xi)合計として素数を得る：

E11=合計として素数を得るイベント。, 合計として素数のイベントはE11==15

したがって、確率ofgetting’合計として素数’

有利な結果の数
P(E11)=可能な結果の総数
=15/36
=5/12

(xii)偶数のadoubletを取得する：

E12=偶数のダブレットを取得するイベント。, 偶数のダブレットのイベントはE12==3になります

したがって、確率ofgetting’偶数のダブレット’

有利な結果の数
P(E12)=可能な結果の総数
=3/36
=1/12

(xiii)一方のダイで2のお守りを取得し、他方のダイで3の倍数を取得する:

E13=2の倍数を取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得するイベントを取得する他のダイ上の3の倍数。, 一方のダイで2の倍数、他方のダイで3の倍数のイベントはE13==11

したがって、”一方のダイで2の倍数、他方のダイで3の倍数”を得る確率

好ましい結果の数
P(E13)=可能な結果の総数
=11/36

4. 二つが投げられる。 （I）和5を得ることに賛成するオッズを見つけ、（ii）和6を得ることに反対するtheoddsを見つけます。

ソリューション：

私たちは、二つのダイの単一のスローで、総数の可能性のある結果は（6×6）=36であることを知っています。

Sを標本空間とする。 すると、n(S)=36である。,

（i）合計5を得ることに賛成するオッズ：

E1を合計5を得るイベントとする。 そして
E1= {(1, 4), (2, 3), (3, 2), (4, 1)}
√P(E1)=4
したがって、P(E1)=n(E1)/n(S)=4/36=1/9
E1=P(E1)を支持する√オッズ)/ = (1/9)/(1 – 1/9) = 1/8.

(ii)和6を得ることに対するオッズ：

E2を和6を得るイベントとする。 そして、
E2= {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
√P(E2)=5
したがって、P(E2)=n(E2)/n(S)=5/36
√E2に対するオッズ=/P(E2) = (1 – 5/36)/(5/36) = 31/5.

5., 二つのサイコロ、青色とオレンジを巻いていた。 得る確率を見つける

（i）両方に等しい数

（ii）合計が9である二つの数がそれらに現れる。,P>

ソリューション：

可能な結果は

(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)

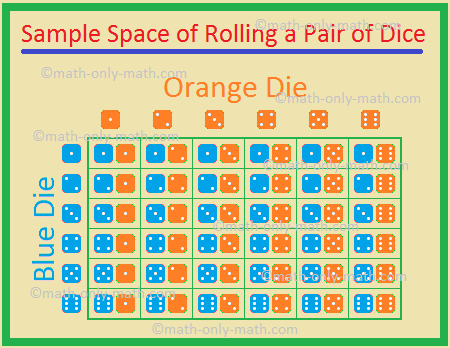
したがって、可能な結果の総数=36です。,

(i)イベントの好ましい結果の数E

=両方のサイコロに等しい数を持つ結果の数

=6。したがって、定義により、P（E）=\（\frac{6}{36}\)

=\(\frac{1}{6}\)

（ii）イベントのための有利な結果の数F

=それらに表示される二つの数字が合計9を持っている結果の数

=4。したがって、定義により、P(F)=\(\frac{4}{36}\)

=\(\frac{1}{9}\)。

これらの例は、ローリングツーサイコロの確率に基づいて、さまざまなタイプの問題を解決するのに役立ちます。,p>Probability and Playing Cards

Probability for Rolling Two Dice

Solved Probability Problems

Probability for Rolling Three Dice

9th Grade Math

From Probability for Rolling Two Dice to HOME PAGE