モバイル通知を表示すべてのノートを表示すべてのノートを非表示
セクション3-1:パラメトリック方程式と曲線
ここまで(微積分Iと微積分IIの両方で)、\(y=f\left(x\right)\)または\(x=h\left(y\right)\)の形式の関数をほぼ独占的に見てきましたが、私たちが開発したほとんどすべての式は、関数がこれら二つの形式のいずれかであることを必要としています。 問題は、私たちが見たいすべての曲線や方程式がこの形式に簡単に落ちるわけではないということです。
例えば、円を取る。 半径\(r\)で原点を中心とする円の方程式を書き留めるのは簡単です。,
\
しかし、上記のいずれの形式でも、円の方程式を単一の方程式として書くことはできません。 \(X\)または\(y\)については、次の二つの式が示すように解くことができます
\
しかし、実際にはこれらのそれぞれに二つの関数があります。 各式は円の一部を与えます。
\
残念ながら、私たちは通常、サークル全体に取り組んでいるか、単にその一部だけに取り組んでいるとは言えません。 もしできれば狭いものだけにこれらの部分の機能はまだしばしばかなり不快にするのに用いられております。,
\
この第三の変数は通常\(t\)で表されます(ここで行ったように)が、もちろんそうである必要はありません。 使用する\(t\)の値を制限することもあれば、そうしないこともあります。これはしばしば問題と私たちが何をしようとしているかに依存します。
パラメトリック曲線が何であるかを視覚化するために、我々は一定の動きにある水の大きなタンクを持っていると私たちはタンクにピンポンボールをドロップすることをふりをしています。, ポイント\(\left({x,y}\right)=\left({f\left(t\right),g\left(t\right)}\right)\)は、時間\(t\)におけるタンク内のピンポンボールの位置を表し、パラメトリック曲線はピンポンボールのすべての これは常に正しい類推ではないことに注意してくださいが、パラメトリック曲線が何であるかを視覚化するのに役立ちます。
パラメトリック曲線をスケッチすることは、必ずしも簡単なことではありません。 例を見て、パラメトリック曲線をスケッチする一つの方法を見てみましょう。, この例では、この方法が通常bestではない理由についても説明します。
この時点で、パラメトリック曲線をスケッチするための唯一のオプションは、\(t\)の値を選択し、それらをパラメトリック方程式に差し込み、点をプロットすることです。 それでは、いくつかの\(t\)のプラグインをしましょう。,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, 残念ながら、現時点ではこの質問に対する本当の答えはありません。 曲線がどのように見えるかについての良いアイデアが得られるとかなり確信するまで、\(t\)を選ぶだけです。 パラメトリック曲線をスケッチするこの方法をより貧しい選択肢の一つにするのは、\(t\)の”良い”値を選ぶことに関するこの問題です。 時々私達に選択の余地がないが、私達に選択があれば私達はそれを避けるべきである。
後の例では、これらの\(t\)の値がどのように選択されたかを説明するのに役立つ別のグラフ化方法について説明します。,
曲線を実際にスケッチする前に、もう一つ議論すべきアイデアがあります。 パラメトリック曲線には動きの方向があります。 運動の方向は、\(t\)を増やすことによって与えられます。 したがって、パラメトリック曲線をプロットするときには、動きの方向を示す矢印も含まれます。 グラフ上の特定の点を与えた\(t\)の値も、その特定の点を与えた\(t\)の値を明確にするために与えることがよくあります。
ここでは、このパラメトリック曲線のスケッチです。
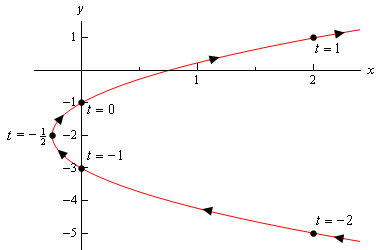
だから、右に開く放物線があるように見えます。,
この例を終わらせる前に、まず議論する必要があるいくらか重要で微妙な点があります。 スケッチの一部があることを示すために、\(t=-2\)と\(t=1\)に対応する点の右側にスケッチの一部を含めるようにしました。 私達がそれらのポイントで単にスケッチを止めたならば、私達は、それらのポイントの右への曲線の部分がなく、明らかに存在するであろうことを示している。 私たちはそれらの点のいずれも計算しませんでした。,
これは重要でないポイントのように見えるかもしれませんが、次の例で見るように、それは私たちが考えるかもしれないよりも重要です。
このグラフをスケッチするためのはるかに簡単な方法に対処する前に、まずパラメータの制限の問題に対処しましょう。 前の例では、パラメーターに制限はありませんでした。 上記のスケッチに示すように、パラメータに制限がなければ、グラフは両方向に継続します。
しかし、パラメータに制限があることが多く、これはパラメトリック方程式のスケッチに影響します。, この効果を確認するには、前の例のわずかな変化を見てみましょう。
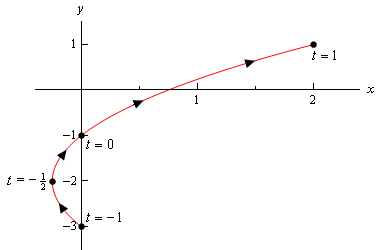
このスケッチでは、\(t\)の範囲の終点から始まる点でスケッチを開始および停止しました。
この場合、曲線は\(t=-1\)から始まり、\(t=1\)で終わりますが、前の例では曲線は実際には計算した右端の点から始まりませんでした。, 曲線がある点で始まる/終わる場合、またはその点が単純に計算した最初/最後のものである場合は、スケッチで明確にする必要があります。
これで、このパラメトリック曲線をスケッチする簡単な方法を見てみましょう。 この方法は、すべてではないが多くの場合において、実際にパラメトリック方程式からパラメータを除去し、\(x\)と\(y\)のみを含む関数を得ることができるという事実を使用しています。 これを元のパラメトリック方程式と区別するために、これを代数方程式と呼ぶことがあります。, この方法には二つの小さな問題がありますが、それらの問題に対処するのは簡単です。 しかし、我々は常にこれを行うことができないことに注意することが重要です。
パラメータをどのように除去するかは、パラメトリック方程式に依存します。 ここまで取り組んできたパラメトリック方程式のセットのパラメータを削除する方法を見てみましょう。
パラメータを削除したら、パラメトリック曲線のスケッチを取得することはかなり簡単です。 我々に必要なのはグラフ方程式を見出を廃止することによりパラメータとします。, しかし、既に述べたように、この方法には二つの小さな問題があります。 最初は動きの方向です。 \(X\)と\(y\)だけを含む方程式は、パラメトリック曲線の動きの方向を与えません。 しかし、これは一般的に修正するのは簡単な問題です。 最後の例のパラメトリック方程式の導関数を簡単に見てみましょう。 それらは、
\
\(x\)導関数は、正と負の両方になるので、この分析には役に立たないので、\(x\)は\(t\)の値に応じて増加と減少の両方になることに注意してください。\(x\)の導関数は、\(t\)の値に応じて増加と減少の両方になります。, どちらの方向の曲線をたどると、\(x\)の増加と減少の両方が表示されるので、それは方向には役に立ちません。
いくつかのケースでは、この例のような方程式の一つだけが方向を与え、他のケースではどちらか一方を使用することができます。 場合によっては、方向を決定するために両方の導関数が必要である可能性もあります。 それは常にパラメトリック方程式の個々のセットに依存します。,
パラメータを削除することに関する第二の問題は、残りの例でこの問題に遭遇するので、例で最もよく説明されています。
さて、それは本当に長い例でした。 これらのタイプの問題のほとんどは長くない。 まだたくさんいてこういうカップルの重要なアイデアを出す。 このセクションの残りの例は、通過するのに時間がかかるべきではありません。
さて、パラメトリック方程式についての重要な考え方を説明する別の例を見てみましょう。,
だから、我々は最後の二つの例で何らかの方法で同じグラフを与えたパラメトリック方程式の二つのセットを見ました。 しかし、彼らはグラフを異なる回数トレースするので、私たちは本当に少なくとも何らかの方法で異なるパラメトリック曲線としてそれらを考える必 これは心配する必要のない違いのように見えるかもしれませんが、後のセクションで見るように、これは非常に重要な違いになる可能性があります。 後のセクションのいくつかでは、正確に一度トレースされる曲線が必要になります。,
他の問題に進む前に、これらの種類のパラメトリック方程式で\(t\)をntに変更することによって何が起こるかを簡単に認識しましょう。 正弦と余弦のみを含むパラメトリック方程式を扱っていて、引数を\(t\)からntに変更すると、それらの両方が同じ引数を持つとき、曲線がトレースされ If\(n>1\)速度を上げ、if\(n<1\)速度を下げます。
それでは、いくつかのより多くの例を見てみましょう。,
この時点までに、\(t\)の十分な範囲を取った場合、パラメータを削除することによって得られた完全なグラフをトレースする例を見てきました。 曲線の一部だけを連続的にトレースするパラメトリック方程式のセットを持つことは可能ではありません。 通常、これが起こるかどうかは、パラメトリック方程式によって課される\(x\)と\(y\)の限界を探すことによって判断できます。,
オブジェクトまたは粒子の経路を記述するためにパラメトリック方程式を使用することがよくあります。 その例を見てみましょう。
この時点で小さな警告を出す必要があります。 それらに関わるアイデアのために、私たちは曲線の一部を何度も後退させるパラメトリック曲線に集中しました。 しかし、これが常に起こるという考えにあまりにもロックされてはいけません。 多くの場合、ほとんどのパラメトリック曲線は一度だけトレースします。 私たちが見た最初のものはこれの良い例です。 このパラメトリック曲線を二度と引き起こさないたの一部又は全部をそのものです。,
先に進む前に、このセクションで議論すべき最後のトピックがあります。 これまでにスタートしていますが、自分たちとパラメトリック方程式のパラメータを決定するパラメトリックカーブとなります。
しかし、私たちは他の道を行きたい時があります。 関数や方程式が与えられた場合、そのためのパラメトリック方程式のセットを書き留めたい場合があります。 これらのケースでは、関数をパラメータ化すると言います。
例4と5を例とすると、楕円(したがって円)に対してこれを行うことができます。, 楕円が与えられると、
\
パラメトリック方程式のセットは、
\
このパラメトリック方程式のセットは、点\(\left({a,0}\right)\)から始まる楕円をトレースし、反時計回りの方向にトレースし、\(0\le t\le2\pi\)の範囲で正確に一度トレースします。 これは、楕円および/または円を扱ういくつかの科目で継続的に使用されているため、かなり重要なパラメトリック方程式のセットです。
すべての曲線は複数の方法でパラメータ化することができます。 次のいずれかも、同じ楕円をパラメータ化します。,
\
\(\omega\)が存在すると、例5で見たように楕円が回転する速度が変わります。 また、最後の二つは時計回りの動きで楕円をトレースすることに注意してください(これを確認したい場合があります)。 また、それらはすべて同じ場所から始まるわけではないことに注意してください(\(t=0\)を出発点として考える場合)。
もちろん楕円のパラメータ化はさらに多くありますが、そのアイデアは得られます。 それぞれのパラメータ化は、\(t\)の範囲が異なる可能性がある曲線を一度トレースすることを覚えておくことが重要です。, 各パラメータ化は、異なる動きの方向で回転し、異なる点から開始することができます。
あなたは、特定の場所で始まり、動きの特定の方向を持っている楕円のパラメータ化が必要であることがわかりますので、いくつかの作業では、あなたが後にしている動作を与えるパラメトリック方程式のセットを書き留めることができることを知っています。
さて、他の重要なパラメータ化のカップルを書き留めてみましょうし、動きの方向、開始点、および\(t\)の一つのトレースの範囲についてのすべてのコメント,
まず、円は楕円の特別なケースに過ぎないので、楕円のパラメータ化を使用して、半径\(r\)の原点を中心とする円のパラメータ方程式を得ることができます。 円をパラメータ化する一つの可能な方法は、
\\
この時点では、このような関数のパラメータ化を行うことはそれほど有用ではないかもしれませんが、関数自体の代わりにパラメータ化を扱うことが実際に容易になるか、または必要になるかもしれない多くの例があります。, 残念なことに、ほぼすべてのこれらのインスタンスで発生する微分積分学IIIコースです。
















コメントを残す