統計定義>
内容:
- 定義
- 絶対値
- 整数プログラミング
定義
整数の集合には、しばしば記号zが与えられ、zは
整数の集合には、シンボルzが与えられ、zは
{…, -3, -2,-1, 0, 1, 2, 3,…}
無限の数の整数があります。, 右の数字は常に左の数字よりも大きくなります。
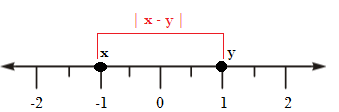
-1と1の間の距離を示す数直線。
整数の絶対値
整数の絶対値は、その数から原点(0)までの距離です。 3と-3の両方が原点から3単位(ステップ)離れているので、両方の数の絶対値は3です。,
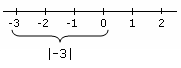
-3の絶対値は3です。
符号
加算と減算
異なる符号を持つ二つの整数を追加するには、絶対値の違いを見つけて、差を与える同じ符号として数
例えば: (-5) + (3)
- 絶対値(5および3)を求めます。
- 5と3の違いを見つけます(5–3=2)。li>
- 最大絶対値の符号を求めます。 -5は負の符号を持つ。,
- ステップ3の記号をステップ2で見つかった差分に追加します。 結果は-2です。
ある整数が他の整数に加算または減算された場合、結果は常に整数になります。
乗算
整数を乗算するには、絶対値を乗算します。 乗算される二つの整数が同じ符号を持つ場合、結果は正になります。 二つの整数が異なる符号を持つ場合、結果は負になります。
ある整数に別の整数が乗算されると、結果は常に整数になります。 しかし、あるものを別のもので割った場合、結果は整数であっても整数でなくてもよい。, たとえば、3/3=1および8/4=2で整数ですが、3/4および8/5は整数ではありません。
整数計画法
整数計画法(IP)問題は、変数の一部(またはすべて)が整数値に制限されている実現可能性または数学的最適化問題の一種です。
- すべての変数が整数に制限されている場合、IP問題は純粋な整数計画問題(ip)と呼ばれます。
- 変数が必要な整数とそのような制限がない他の変数との混合物である場合、IP問題は混合IP問題と呼ばれます。,
- 整数が0または1に制限されている場合、問題は純粋または混合&mdas;バイナリ整数計画問題と呼ばれます。
IPという用語は、整数線形計画法、目的関数と非整数制約の両方が線形であるプログラミングの一種を指すために使用されることがあります。
IPの問題によるモデリング
しかし、IPの問題はいつ使用されますか? 値が自然に整数に制限されている現実の問題をモデル化することがよくあります。, たとえば、単純な線形計画法モデルで中国の工場でのコンピュータ生産をモデル化すると、月に2067.4台のコンピュータの計画が思いつくかもしれません。 ということです。4″は直感的な意味をなさない;どのように工場がコンピュータの40%を生産することができます(私は彼らがそのときにラインを停止することができコンピュータの4つが完成しました!). 私たちはそれを丸めることができますが、そもそも整数であれば好むでしょう。
整数以外の変数が意味をなさないことがあります。 たとえば、教師を特定の都市に割り当てる線形計画法モデルでは、0を配置することを推奨します。,ある町で7人の教師と別の町で0.5人の教師。 一部またはすべての変数の整数を考慮したモデルを作成する方法が必要です。
IP問題の策定と解決
Ipの策定は、通常、単純な線形プログラムの策定よりも困難です。 いくつかのトリックがありますが、キーは練習です。
線形プログラムに使用されるものと同様のIpを解くための汎用の計算効率の高いアルゴリズムはありません。, 代わりに、通常は、汎用の計算上非効ineffectiveな解法方法を選択するか、この特定の問題だけを攻撃できる特別な目的のアルゴリズムを設計する必要があ
ステファニー-グレン。 “整数、絶対値:簡単な定義と例、プログラミング”からStatisticsHowTo.com:私たちの残りの部分のための基本統計! https://www.statisticshowto.com/integer/
——————————————————————————
宿題やテストの質問に助けが必要ですか?, Chegg Studyを使用すると、その分野の専門家からあなたの質問に対するステップバイステップの解決策を得ることができます。 Cheggの家庭教師とのあなたの最初の30分は無料です!
















コメントを残す