Vektorit ovat laajasti hyödyllisiä tieteen kuvaamaan mitään, joilla on sekä suunta sekä suuruus. Ne piirretään yleensä suippojen nuolien avulla, joiden pituus edustaa vektorin suuruutta. Pelinrakentajan syöttö on yksinkertainen esimerkki, koska sillä on suunta yleensä jossain alakentällä ja magnitudi. Joskus meidän täytyy käsitellä kahta vektoria yhdessä työstäen jotain esinettä. Tällaisissa tapauksissa näiden vektorien väliset kulmat ovat tärkeitä., Tämä aihe selittää kulma kahden vektorit kaava sekä esimerkkejä. Oppikaamme se!
käsite vektorit
kentän ulkopuolella vektoreita voidaan käyttää kuvaamaan mitä tahansa määrää fyysisiä esineitä tai toimintoja. Esimerkiksi. Esimerkiksi tuuli on vektoriaalinen määrä. Se johtuu siitä, että missä tahansa paikassa sillä on suunta sekä suuruus. Voimme tehdä kartan ilmavirrasta milloin tahansa, sitten piirtämällä tuulivektorit useisiin eri maantieteellisiin paikkoihin.
monet liikkuvien esineiden ominaisuudet ovat myös eräänlaisia vektoreita., Biljardipallossa sen nopeusvektori kuvaa sen liikettä. Se näyttää suunnan vektori nuoli markkaa liikkeen suuntaan, ja vektorin pituus edustaa nopeutta pallo.
biljardipallon momentum on myös esimerkki vektoriaalisesta määrästä. Koska se on yhtä suuri kuin massa kertaa nopeus. Siksi, vauhtia vektori mustekynä samaan suuntaan kuin sen nopeusvektori. Liikevektorin suuruus on pallon nopeuden ja massan kertotuote.,
matematiikan kannalta vektori on mikä tahansa olio, jolla on määritettävissä oleva magnitudi ja suunta. Koska vektorit eivät ole samat kuin standardin linjat tai muotoja, meidän täytyy käyttää joitakin erityisiä kaavoja löytää kulmat niiden välillä.
Kaava välinen Kulma Kahden vektorin
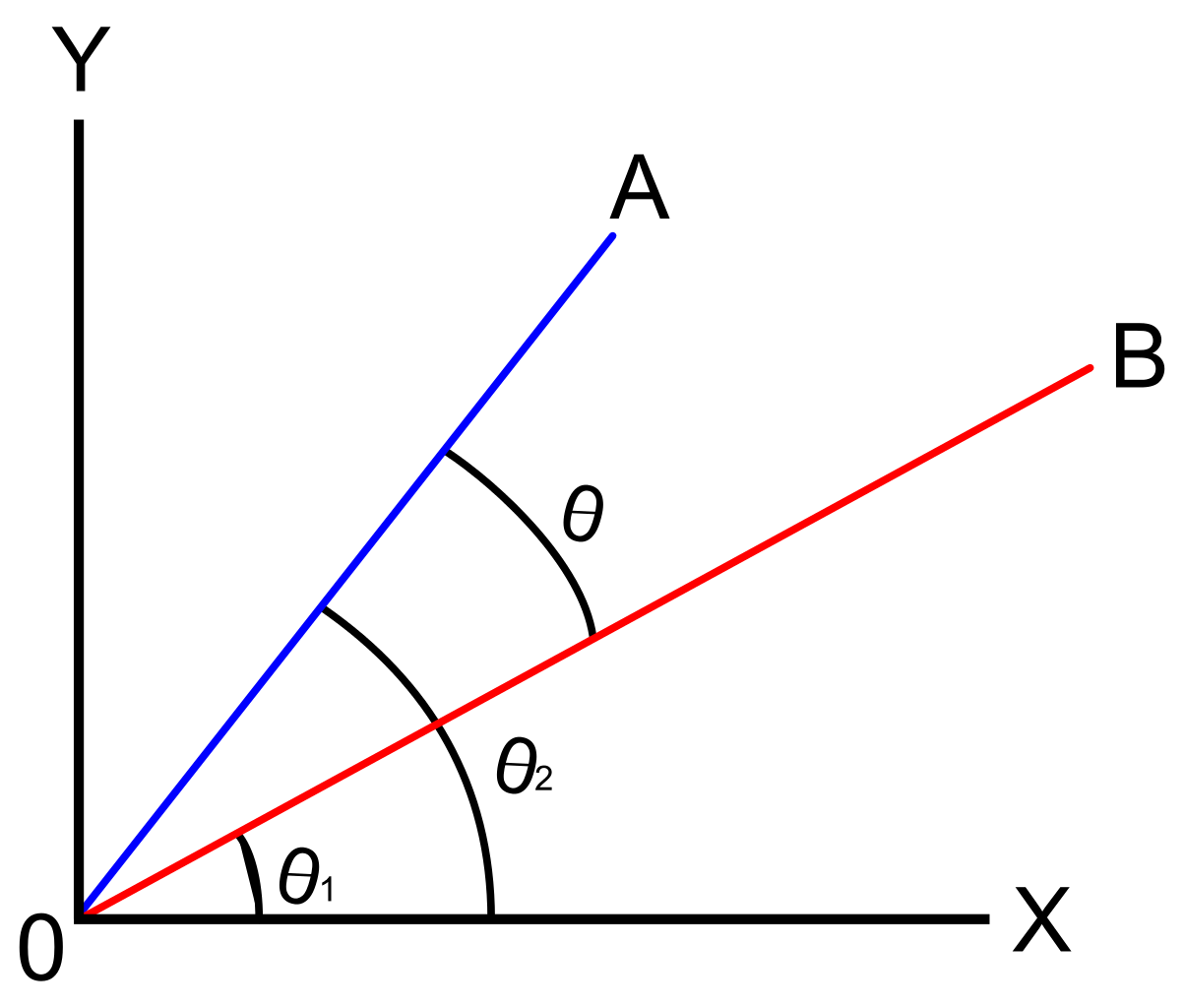
välinen kulma kahden vektorin lykätään yhden pisteen, joka on nimeltään lyhin kulma, jossa meidän täytyy kääntyä yksi vektoreita, asema co-suuntaava toinen vektori.,
vektorien suuntakulmia koskeva keskustelu keskittyy vektorin kulman löytämiseen positiivisen x-akselin suhteen. Tämä keskittyy kahden vektorin väliseen kulmaan vakioasennossa. Vektorin sanotaan olevan vakioasennossa, jos sen alkupiste on alkuperä (0, 0).
Jos kaksi vektoria ovat olettaneet, kuten a ja b, sitten piste luotu on määritelty .b.oletetaan, että nämä kaksi vektoria erotetaan kulmalla \(\theta\). Tietää, mitä on kulman mittaus meidän tulee ratkaista avulla kaava antaa:
Me tiedämme, dot tuote:
\(\vec{a}.,\vec{b} =|\vec{a}||\vec{b}|cos\theta\)
Nyt, välinen kulma kahden vektorin kaava on:
\(\theta = cos^{-1}\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}\)
Missä \\(theta\) on kulma a ja b vektoreita.
Ratkaista Esimerkkejä välinen Kulma Kahden vektorin Kaava
Q. 1: Laske välinen kulma kahden vektorin 3i + 4j – k ja 2i – j + k.
Ratkaisu:
a = 3i + 4j – k ja
b = 2i – j + k,
Me määrittelemme dot tuote:
a .b = (3i + 4j – k).(2i-j + k)
















Vastaa