Todennäköisyys liikkuvan kaksi noppaa yhdessä kuusi puolinen dotssuch kuin 1, 2, 3, 4, 5 ja 6 pisteet kunkin kuolla.

Kun kaksi noppaa on heitetään samanaikaisesti, mikä määrä tapahtuma voi olla 62 = 36, koska jokainen kuolee on 1 6 määrä sen kasvoja. Mahdolliset tulokset esitetään seuraavassa taulukossa.,
Todennäköisyys – Näyte tilaa kaksi noppaa (tulokset):
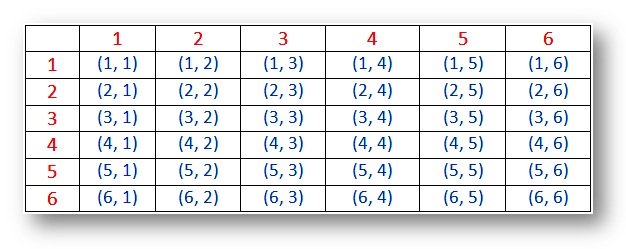
Huomautus:
(en) tulokset (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) ja (6, 6) kutsutaan doublets.
(ii) pari (1, 2) ja (2, 1) ovat eri tuloksia.
Toimi-out-ongelmia, joihin todennäköisyyden liikkuvan kaksi noppaa:
1. Kaksi noppaa on rullattu. Olkoon A, B, C tapahtumia saada summa 2, summa 3 ja summa 4 vastaavasti., Sitten, osoittavat, että
(en) on yksinkertainen tapahtuma.
(ii) B-ja C-yhdiste, tapahtumat
(iii) A ja B ovat toisensa poissulkevia
Ratkaisu:
– on Selvää, että meidän on
A = {(1, 1)}, B = {(1, 2), (2, 1)} ja C = {(1, 3), (3, 1), (2, 2)}.
(i) koska A koostuu yhdestä näytepisteestä, se on yksinkertainen tapahtuma.
(ii) koska sekä B että C sisältävät useamman kuin yhden näytepisteen, jokainen niistä on yhdistetapahtuma.
(iii) Koska A ∩ B = ∅, A ja B ovat toisensa poissulkevia.
2. Kaksi noppaa on rullattu., A on tapahtuma, että summa numerot näkyvät kaksi noppaa on 5, ja B on tapahtuma, että ainakin yksi noppaa näyttää jopa 3.
ovatko nämä kaksi tapahtumaa I) toisensa poissulkevia, ii) tyhjentäviä? Perustelkaa vastauksenne.
Ratkaisu:
Kun kaksi noppaa on rullattu, meillä on n(S) = (6 × 6) = 36.
Nyt, = {(1, 4), (2, 3), (4, 1), (3, 2)}, ja
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.
näin ollen A ja B eivät sulje toisiaan pois.,
(ii) myös A ∪ B ≠ S.
siksi A ja B eivät ole tyhjentäviä tapahtumia.
Lisää esimerkkejä liittyvät kysymykset todennäköisyydet heittää kahta noppaa.
3. Kaksi noppaa heitetään samanaikaisesti.,) saada jakku
(v) saada summa 8
(vi) saada summa jaollinen 5
(vii) saada summa vähintään 11
(viii) saada useita 3 summa
(ix) saada yhteensä ainakin 10
(x) on yhtä suuri kuin summa
(xi) saada ensisijainen määrä kuin summa
(xii) saada jakku jopa numeroita
(xiii) saada useita 2 on yksi kuolee ja useita 3 toisaalta die
Ratkaisu:
Kaksi eri noppaa heitetään samanaikaisesti olla numero 1, 2, 3, 4, 5 ja 6 kasvoillaan., Tiedämme, että yhdellä heitetään kaksi eri noppaa, kokonaismäärä mahdolliset tulokset on (6 × 6) = 36.
(i) kuuden saaminen tuotteeksi:
Let E1 = event of getting six as a product. Määrä, jonka tuote on kuusi on E1 = = 4
näin Ollen, todennäköisyys ofgetting kuuden tuote’
Useita suotuisia tuloksia
P(E1) = Kokonaismäärä mahdollinen lopputulos.
= 4/36
= 1/9
(ii) saada summa ≤ 3:
E2 = tapahtuma saada summa ≤ 3., Määrä, joiden summa on ≤ 3 on E2 = = 3
näin Ollen, todennäköisyys ofgetting ’summa ≤ 3’
Useita suotuisia tuloksia
P(E2) = Kokonaismäärä mahdollinen lopputulos.
= 3/36
= 1/12
(iii) saada summa ≤ 10:
E3 = tapahtuma saada summa ≤ 10. Määrä, joiden summa on ≤ 10 E3 = = 33
näin Ollen, todennäköisyys ofgetting ’summa ≤ 10’
Useita suotuisia tuloksia
P(E3) = Kokonaismäärä mahdollinen lopputulos.
= 33/36
= 11/12
(iv)saada jakku:Anna E4 = tapahtuma saada jakku., Numero, joka jakku on E4 = = 6
näin Ollen, todennäköisyys ofgetting ’kaksinkertainen’
Useita suotuisia tuloksia
P(E4) = Kokonaismäärä mahdollinen lopputulos.
= 6/36
= 1/6
(v)saada summa 8:
E5 = tapahtuma saada summa 8. Numero, joka on summa 8 E5 = = 5
näin Ollen, todennäköisyys ofgetting ’summa 8’
Useita suotuisia tuloksia
P(E5) = Kokonaismäärä mahdollinen lopputulos.
= 5/36
(vi)saada summa on jaollinen 5:
Anna E6 = tapahtuma saada summa jaollinen 5., Määrä, joiden summa on jaollinen 5: E6 = = 7
näin Ollen, todennäköisyys ofgetting ’summa jaollinen 5’
Useita suotuisia tuloksia
P(E6) = Kokonaismäärä mahdollinen lopputulos.
= 7/36
(vii)saada summa atleast 11:
Anna E7 = tapahtuma saada summa vähintään 11. Tapahtumien summa vähintään 11 on E7 = = 3
näin Ollen, todennäköisyys ofgetting ’summa vähintään 11’
Useita suotuisia tuloksia
P(E7) = Kokonaismäärä mahdollinen lopputulos.
= 3/36
= 1/12
(viii) saada luultavasti tämän 3 summa:
E8 = tapahtuma saada useita 3 summa., Tapahtumia useita 3 summa on E8 = = 12
näin Ollen, todennäköisyys ofgetting ’useita 3 summa’
Useita suotuisia tuloksia
P(E8) = Kokonaismäärä mahdollinen lopputulos.
= 12/36
= 1/3
(ix) saada yhteensä vähintään 10:
Anna E9 = tapahtuma saada yhteensä vähintään 10., Tapahtumia yhteensä vähintään 10 tulee olla E9 = = 6
näin Ollen, todennäköisyys ofgetting ’yhteensä vähintään 10’
Useita suotuisia tuloksia
P(E9) = Kokonaismäärä mahdollinen lopputulos.
= 6/36
= 1/6
(x) tulossa evennumber summa:
E10 = tapahtuma saada parillinen määrä kuin summa., Tapahtumat parillinen määrä kuin summa tulee E10 = = 18
näin Ollen, todennäköisyys ofgetting ’parillinen määrä kuin summa
Useita suotuisia tuloksia
P(E10) = Kokonaismäärä mahdollinen lopputulos.
= 18/36
= 1/2
(xi) saada primenumber summa:
E11 = tapahtuma saada ensisijainen määrä kuin summa., Tapahtumat alkuluku, koska summa on E11 = = 15
näin Ollen, todennäköisyys ofgetting ’alkuluku, koska summa’
Useita suotuisia tuloksia
P(E11) = Kokonaismäärä mahdollinen lopputulos.
= 15/36
= 5/12
(xii) saada adoublet jopa numeroita:
Anna E12 = tapahtuma saada jakku jopa numeroita., Tapahtumat jakku jopa numerot E12 = = 3
näin Ollen, todennäköisyys ofgetting ’jakku jopa numerot’
Useita suotuisia tuloksia
P(E12) = Kokonaismäärä mahdollinen lopputulos.
= 3/36
= 1/12
(xiii) saada luultavasti tämän 2 on yksi kuolee ja useita 3 toisaalta kuolla:
Anna E13 = tapahtuma saada useita 2 on yksi kuolee ja useita 3 toisaalta kuolla., Tapahtumia on useita 2 on yksi kuolee ja useita 3 muut kuolevat E13 = = 11
näin Ollen, todennäköisyys ofgetting ’jaollinen 2: yksi kuolee ja useita 3 toisaalta kuolla’
Useita suotuisia tuloksia
P(E13) = Kokonaismäärä mahdollinen lopputulos.
= 11/36
4. Twodice heitetään. Etsi (en) kertoimet hyväksi saada summa 5, ja (ii) theodds vastaan saada summa 6.
ratkaisu:
tiedämme, että yhdellä heitolla kaksi kuolee, mahdollisten lopputulosten kokonaismäärä on (6 × 6) = 36.
olkoon s näyteavaruus. Sitten n (S) = 36.,
(i) kertoimet summan saamisen puolesta 5:
olkoon E1 summa 5. Sitten,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P(E1) = 4
näin Ollen P(E1) = n(E1)/n(S) = 4/36 = 1/9
⇒ kertoimet hyväksi E1 = P(E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii) kerroin summan saamista vastaan 6:
olkoon E2 summa 6. Sitten,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P(E2) = 5
Siksi, P(E2) = n(E2)/n(S) = 5/36
⇒ kertoimet vastaan E2 = /P(E2) = (1 – 5/36)/(5/36) = 31/5.
5., Kaksi noppaa, yksi sininen ja yksi oranssi, rullataan samanaikaisesti. Löytää todennäköisyys saada
(en) yhtä paljon molemmilla.
(ii) kaksi numeroa näy ne, joiden summa on 9.,
Ratkaisu:
mahdolliset tulokset,
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
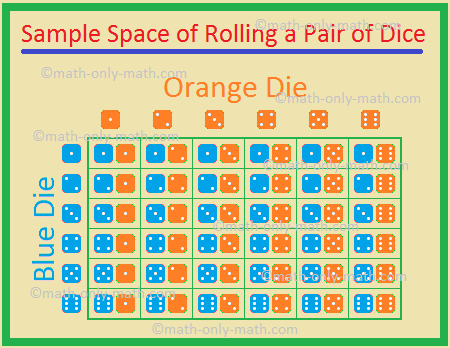
näin Ollen kokonaismäärä mahdolliset tulokset = 36.,
(i) tapahtumalle suotuisien tulosten lukumäärä e
= niiden tulosten lukumäärä, joilla on sama määrä molemmilla nopilla
= 6 .
Niin, määritelmän mukaan P(E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) Useita suotuisia tuloksia tapahtuman F
= Useita tuloksia, joissa kaksi numeroa näy niitä on summa 9
= 4 .
Näin ollen määritelmän mukaan P(F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
nämä esimerkit auttavat ratkomaan erityyppisiä ongelmia rollingtwo-nopan todennäköisyyden perusteella.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Vastaa