Pituus Lävistäjä Yksikön Neliö

pituus lävistäjä yksikön neliö on yhtä suuri kuin neliöjuuri 2.

yksikön neliön lävistäjän pituus on √2. Tämä ei ole hyvä uutinen. Jokainen, joka koskaan törmännyt Pythagoraan lause on tietoinen siitä., Isosceles oikea kolmio jalat pituus 1, hypotenuusan mukaan Pythagoraan lause-12 + 12 = (hypotenuse)2 – On todellakin pituus √2. Motivaatio tämän sivun ei ole niin paljon, että tosiasia itse, mutta tapa osoittaa sen turvautumatta kuuluisa lause. Itse asiassa, se voitaisiin väittää, että Pythagoraan lause olisi voinut käyttää liikaa, katso utelias esimerkki.

argumentti, joka menee takaisin kuva piirtänyt Sokrates Platonin Meno saattaa olla tunnettu Pythagoras itse, vaikka tämä asui vuosisataa aiemmin.,

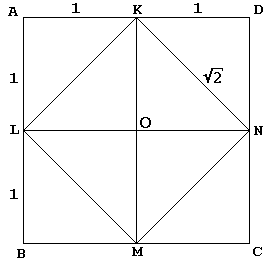
– valintaikkunassa, Sokrates, hänen tavalliseen tapaan, johtaa nuori orja rakentaminen neliön kahdesti alue annetaan yksi:

koska neliö KLMN center O on ensin leikata sen lävistäjät osaksi 4 yhtä kolmioita. Sokrates embeds KLMN osaksi isompi neliö ABCD ikään kuin heijastaa nämä kolmiot kukin sen hypotenuse. Orja sitten myöntää ja kuka ei? – ABCD on kaksi kertaa isompi kuin klmn.

totuus kerrottakoon, Sokrateen neliö ABCD mitattiin 4 kyljessä siten, että neliö KLMN oli pinta-alaltaan 8., On selvää, että kun aloitamme neliön ABCD sivulla 2 (ja siten alue 4), neliö KLMN on alueella 2.

nyt yleisesti positiivisen luvun A osalta √A määritellään numeroksi, jonka neliö on a:

(√a)2.

toisaalta jokainen alueiden opiskelija tietää, että B-puolen neliön pinta-ala on B2. Tästä seuraa, että puolella neliön pinta-ala A on täsmälleen √A. päätämme, että puolella neliön KLMN on √2. Yksi,

– KN = √A.

keskeinen väite on se, että kaaviossa, KN on kaksinkertainen rooli., Sen lisäksi, että yksi puolin neliön KLMN, se toimii myös lävistäjä neliön OKDN. Jälkimmäinen on tietysti yksikköaukio, mikä todistaa väitteemme.

(hieman eri näkökulmasta sama jakso mainitaan muualla.)