Kun kolmion kulmat eivät laske 180 asteeseen

1. Johdanto

lisäävätkö kolmion kulmat jopa 180 astetta tai $\pi$ radiaanit? Vastaus on joskus kyllä, joskus ei. Onko tämä tärkeä kysymys? Kyllä, koska se johtaa käsitys, että on olemassa eri geometriat perustuvat eri aksioomat ” tai ”pelisäännöt geometria’. Onko kysymys merkityksellinen? No ei, ei ainakaan ennen kuin olemme sopineet, tarkoittavat sanat ’kulma’ ja’triangle’, ei ennen kuin tiedämme pelisäännöt., Tässä artikkelissa, me lyhyesti keskustella taustalla aksioomat ja antaa yksinkertainen todiste siitä, että kulmien summa kolmion pinta-yksikkö alalla ei ole yhtä suuri kuin $\pi$, mutta $\pi$ plus kolmion pinta-ala. Käytämme sitä, että pinta-ala yksikön pallo on $4\pi$.

2. Iso Lause

Ennen kuin voimme sanoa, mitä kolmio on meidän päästävä yhteisymmärrykseen siitä, mitä me tarkoitamme pisteitä ja viivoja. Työskentelemme pallogeometriassa (kirjaimellisesti geometria pallon pinnalla)., Tässä geometria tilaa on pinta-alalla; pisteet ovat pisteitä, että pinta, ja viiva on lyhin etäisyys kahden pisteen välillä on suuri ympyrä, joka sisältää kaksi pistettä. Suuri ympyrä (kuten päiväntasaaja) leikkaa pallon kahteen yhtä suureen pallonpuoliskoon. Tällä geometrialla on selviä sovellutuksia etäisyyksiin maan päällä olevien paikkojen ja ilmareittien välillä.,

Pyörivä pallo osoittaa suuri ympyrä

välinen kulma kaksi suurta ympyrää pisteessä P on Euklidinen välinen kulma suuntiin piireissä (tai tiukasti välillä tangentit, piireissä P). Tämä ei aiheuta vaikeuksia suunnistaa maan päällä, koska jossain tietyssä pisteessä ajattelemme kahden suunnan välistä kulmaa ikään kuin Maa olisi siinä pisteessä Tasainen.

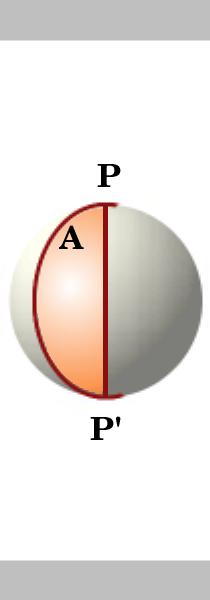
a lune on pallopinnan osa, jota rajoittaa kaksi suurta ympyrää, jotka kohtaavat antipodaalipisteissä., Ensin tarkastellaan alueen lune ja sitten käyttöön toinen suuri ympyrä, joka jakaa lune kolmioihin.

Pyörivä pallo osoittaa 4 lunes

Lemma.

alueen lune ympyrä-yksikön säde on kaksi kertaa kulma,, joka on, jos kulma lune on sitten sen pinta-ala on 2A. Kaksi suurta ympyrää leikkaavat klo vastakkaisia pistettä P ja P’ jakaa pallon 4 lunes. Pinta-ala yksikön pallo on $4\pi$.,

alueilla lunes ovat suhteessa niiden kulmat P joten alueen lune, jonka kulma on

${\frac{A}{2\pi}\times {4\pi}= {2A}}$

tehtävä 1.

mitkä ovat muiden 3 luunan alueet? Onko 4 alueet yhteen $4\pi$?

Tarkista vastauksesi täältä .

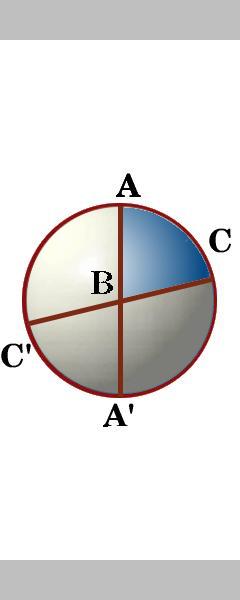
kolmion ABC sivut ovat segmenttejä kolmesta suuresta ympyrästä, jotka itse asiassa leikkaavat pallon pinnan kahdeksaksi pallomaiseksi kolmioksi. Kahden suuren ympyrän välissä pisteen A kautta on neljä kulmaa., Meidän etiketti kulma sisällä kuin kolmion ABC kulma A, ja samoin muut kulmat kolmion ABC kuin kulma B ja kulma C.

Pyörivä pallo osoittaa 8 kolmiota,

Harjoitus 2

Pyörivä pallo voit nimetä kahdeksan kolmioita ja sanoa, onko jokin niistä on samalla alueella? Katso vastauksesi täältä .

lause.

Harkitse pallomainen kolmio ABC on yksikkö pallo, jossa kulmat A, B ja C. Sitten alueen kolmio ABC on

A + B + C – $\pi$.,

kaaviossa näkyy alaspäin katsova näkymä pallonpuoliskolta, jonka rajana on viiva AC: n kautta. Merkityt alueet Alue 1 ja Alue 3 ovat kulmia A ja C vastaavasti. Ajatelkaa mielipuolia B: n ja B: n kautta. Kolmio ABC on congruent-kolmio A ’ B ’C’ niin, että rusetti muotoinen varjostettu alue, merkitty Alue 2, joka on summa aloilla, kolmiot ABC ja’BC’, on yhtä suuri thearea, että lune kulma B, joka on yhtä suuri kuin 2B.,

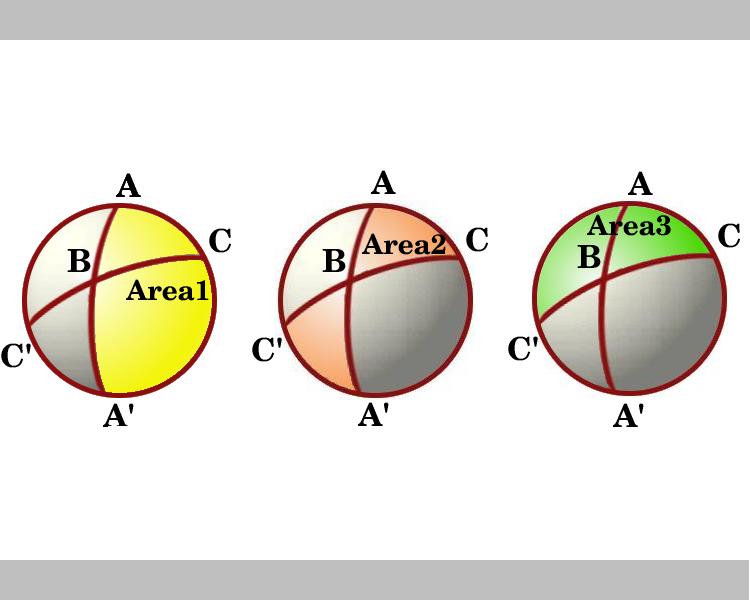
kuvassa näemme alueilla kolme lunes ja käyttää lemma, nämä ovat:

pinta-Ala 1 = 2A
Alue 2 = 2B
Alue 3 = 2C

lisäämällä nämä kolme aluetta ovat alueen kolmion ABC kolme kertaa., Hence

3., Epäeuklidinen geometria

joskus vallankumoukselliset löydöt eivät ole mitään muuta kuin sen näkemistä, mitä nenämme alla on ollut koko ajan. Tämä oli tapaus yli löytö Epäeuklidinen geometria 1800-luvulla. Jostain 2000 vuotta Eukleideksen jälkeen, kirjoitti hänen ”Osatekijät” vuonna 325 EAA ihmiset yrittivät todistaa rinnakkaisen postulate kuin lause, geometria muut aksioomat, mutta aina epäonnistui, ja tämä pitkä tarina., Samaan aikaan matemaatikot käyttivät pallomainen geometria koko ajan, geometria, joka tottelee muut aksioomat, Euklidinen Geometria ja sisältää monia samoja teoreemojen, mutta joka rinnakkaisen postulate ei pidä. Koko ajan heillä oli esimerkki Epäeuklidisesta geometriasta nenänsä alla.

Ajattele line L ja piste P ei L. iso kysymys on: ”Kuinka monta riviä voidaan vetää läpi P yhdensuuntainen L?”Euklidinen Geometria vastaus on `täsmälleen yksi”, ja tämä on yksi versio parallel postulate., Jos summa kulmat jokaisen kolmion geometrian on $\pi$ radians sitten rinnakkainen postulate pitää ja päinvastoin, kaksi ominaisuutta ovat vastaavia.

pallomainen geometria, perus aksioomat, jotka oletamme (pelin säännöt) ovat erilaisia kuin Euklidinen Geometria – tämä on epäeuklidinen Geometria. Olemme nähneet, että pallomainen geometria kulmat kolmiot eivät aina lisätä jopa $\pi$ radiaaneina, joten emme odota rinnakkaisen postulate pitää., Pallogeometriassa suorat (lyhyimmän matkan tai Geodesian viivat) ovat suuria ympyröitä ja geometrian jokainen viiva leikkaa joka toisen viivan kahtena pisteenä. Vastaus isoon kysymykseen siitä, parallels on`Jos meillä on linja, L ja piste P ei L niin ei ole viivoja kautta P yhdensuuntainen L.,”

kreikan matemaatikot (esimerkiksi Ptolemaios c 150) lasketaan mittaukset oikea kulma pallomaiset kolmiot ja työskennellyt kaavat pallotrigonometria ja Arabien matemaatikot (esimerkiksi Jabir ibn Aflah c 1125 ja Nasir ed-din c 1250) laajentaa työtä entisestään. Tässä artikkelissa käsitellyn kaavan löysi Harriot vuonna 1603 ja julkaisi Girard vuonna 1629. Aiheen jatko-osia kehitti Saccerhi (1667 – 1733).,

Kaikki tämä meni pitkälti un-huomannut 19th century discoverers hyperbolinen geometria, joka on toinen epäeuklidinen Geometria, jossa rinnakkaisen postulate ei pidä. Vuonna pallomainen geometria (kutsutaan myös elliptinen geometria) kulmat, kolmiot, lisätä jopa enemmän kuin $\pi$ radiaaneina ja hyperbolinen geometria, kulmat, kolmiot, lisätä jopa vähemmän kuin $\pi$ radiaaneina.

lisää luettavaa Katso Alan Beardonin artikkeli ” Kuinka monta geometriaa on olemassa?”ja Keith Carnen kirjoitus ”outoja geometrioita”., On olemassa joitakin käytännön toimia, jotka voit kokeilla itse tutkia näitä kuvioita edelleen osoitteessa http://nrich.maths.org/MOTIVATE/conf8/index.html