Kolmion Kuva Kulma-Sivu-Kulma (ASA)
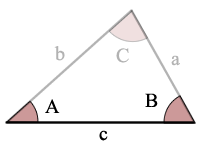
A = kulma
B = kulma B
C = kulma C
a = puolella
b =, b-puolen
c = puoli c
P = kehä
s = semi-perimeter
K = alue
r = säde piirretyn ympyrän.
R = säde rajattujen ympyrä
Laskimen Käyttö
Jokainen laskelma-vaihtoehto, joka näkyy alla, on sub-luoteja, jotka luetellaan järjestyksessä menetelmiä käytetään tässä laskin ratkaista tuntematon kulma ja sivu-arvot mukaan lukien Summa Kulmien Kolmio, sinilause ja kosinilause., Nämä eivät ole ainoat sekvenssit voit käyttää ratkaisemaan tämäntyyppisiä ongelmia.
- Katso myös nämä Trigonometrian Laskimet:
- kosinilause Laskin
- Laki Sines Laskin
Ratkaiseminen Kolmio Lauseet
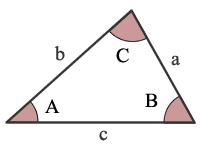
AAA on Kulma, Kulma, Kulma
Määrittäminen kolmen kulmien kolmio ei yksilöi yksi kolmio. Siksi, täsmentämällä kaksi kulmaa tringle voit laskea kolmannen kulman vain.,
kun otetaan huomioon kolmion 2 kulman koot, voidaan laskea kolmannen kulman koko. Kokonaissumma on 180° tai π radiaania.
C = 180° – A – B (asteina)
C = d – A – B (radiaaneina)
AAS on Kulma, Kulma, Puolella
Koska koko 2 kulmat ja 1 vastakkaisella puolella yksi annettu kulmat, voit laskea kokoja jäljellä 1 kulma ja 2 puolta.
käytä Summa Kulmat Sääntö löytää toinen kulma, ja sitten
käytä sinilause ratkaista kunkin muut osapuolet.,
ASA on Kulma, Sivu, Kulma
Koska koko 2 kulmat ja koko se puoli, joka on näiden 2 kulmat voit laskea kokoja jäljellä 1 kulma ja 2 puolta.
käytä Summa Kulmat Sääntö löytää toinen kulma, ja sitten
käytä sinilause ratkaista kunkin muut osapuolet.,
PERSE (tai SSA) on Kulma, Puolella, Puolelle
Koska koko 2 puolin (a ja c, missä a < c) ja koko kulma, joka ei ole niiden välillä, 2 puolta saatat pystyä laskemaan kokoja jäljellä 1 puolella ja 2 näkökulmista, riippuen seuraavia ehtoja.,f Cosines ratkaista kunkin kahden muun kulman
nykyinen 2 täyttä ratkaisuja
Esimerkki: 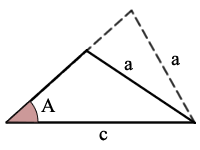
sin(A) = a/c, on yksi mahdollinen kolmio
käytä sinilause ratkaista kulma, C
käytä Summa Kulmat Sääntö löytää toinen kulma, B,
käytä sinilause ratkaisemaan viimeiset puoli, b,
Esimerkki: 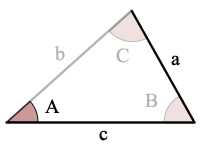
sin(A) > a/c, ei ole mahdollista kolmiot
Virhe Ilmoitus: sin(A) > a/c, niin on olemassa ratkaisuja ja ei ole kolmio!,
Esimerkki: 
SAS on Puolella, Kulmassa, Puoli
Koska koko 2 puolin (c ja a) ja koko kulma B, joka on välillä 2 puolta voit laskea kokoja jäljellä 1 puolella ja 2 näkökulmista.
käytä kosinilause ratkaisemaan jäljellä puolella, b,
selvitä, mikä puoli, a tai c, on pienin ja käyttää sinilause ratkaista koko vastakkaiseen kulmaan, tai C vastaavasti.,
käytä Summa Kulmat Sääntö löytää viimeinen kulma
SSS on Side, Puolella, Puolelle
Koska koot 3 puolelta voit laskea koot kaikki 3 kulmat kolmion.
käytä kulmien ratkaisemiseen kosinien lakia. Voit myös käyttää Summa Kulmat Sääntö löytää lopullinen kulma kun tiedät, 2 ne.,sin-1
kosinilause
Jos a, b ja c ovat pituudet jalat kolmion vastapäätä kulmat A, B ja C vastaavasti; sitten kosinilause seuraavaa:
a2 = c2 + b2 – 2bc cos A, ratkaista cos A, cos A = ( b2 + c2 – a2 ) / 2bc
b2 = a2 + c2 – 2ca, koska B, ratkaista cos B cos B = ( c2 + a2 – b2 ) / 2ca
c2 = b2 + a2 – 2ab cos C, ratkaista cos C cos C = ( a2 + b2 – c2 ) / 2ab
Ratkaista, esimerkiksi kulma, A = cos-1
toisen Kolmion Ominaisuudet
Kolmio kehä, P = a + b + c
Kolmio semi-perimeter, s = 0.,5 * (a + b + c)
Kolmion alueella, K = √
Säde piirretyn ympyrän, kolmion, r = √
Säde rajattu ympyrä, kolmio, R = (abc) / (4K)
Viitteet/ kirjallisuutta
Weisstein, Eric W. ”PERSE Lause.”From MathWorld – A Wolfram Web Resource. Perse lause.
Math is Fun-Solving Sas Triangles
















Vastaa