Kupera ja Kovera Monikulmio

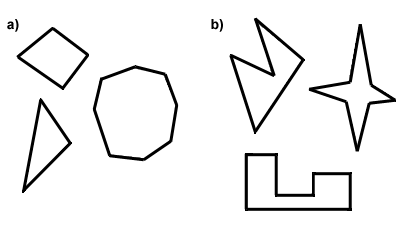
Jokainen monikulmio on joko kupera tai kovera. Kuperien ja koverien monikulmioiden välinen ero on niiden kulmien mittauksissa. Jotta monikulmio olisi konveksi, sen kaikkien sisäkulmien on oltava alle 180 astetta. Muuten monikulmio onconcave. Toinen tapa ajatella on, että se on tämä: lävistäjät on convexpolygon kaikki sisätilojen monikulmio, ottaa huomioon, että tietyt lävistäjien kovera monikulmio valhe ulkopuolella monikulmio, sen ulkoa., Below in Part A are some convex polygons, and in Part B, some concave polygons. In the rest of this text, you can assume that every polygon discussed is convex.

Figure %: Convex and concave polygons

Regular Polygons

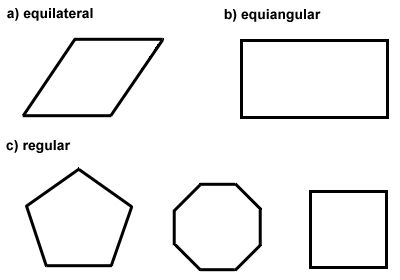
Polygons can also be classified as equilateral, equiangular, or both. Equilateral polygons have congruent sides, like a rhombus. Equiangular polygons have congruent interior angles, like a rectangle., Kun monikulmio on sekä tasasivuinen että ekviangulaarinen, sitä kutsutaan säännölliseksi monikulmioksi. Neliö on esimerkki säännöllisestä monikulmiosta. Säännöllisen monikulmion keskipiste on piste, josta kaikki monikulmion kärkipisteet ovat yhtä kaukana toisistaan. Tavallisilla polygoneilla on erityisiä ominaisuuksia, joita tutkimme seuraavassa jaksossa. Alla on joitakin esimerkkejä ekviangulaarisista, tasasivuisista ja säännöllisistä monikulmioista.,

Figure %: Equilateral, equiangular, and regular polygons

Congruent Polygons

One more note on polygons: Polygons whose sides are all congruent are congruent polygons. Knowing this term will be important later. In congruent polygons, every segment is congruent.