vektori, joka on suuruudeltaan (kuinka kauan se on) ja suunta:
Tässä on kaksi vektorit:

Ne voivat olla kerrottuna käyttämällä ”pistetulo” (katso myös Cross-Tuote).,
Voimme laskea pistetulo kahden vektorin näin:

a · b = |a| × |b| × cos(θ)
Missä:
|a| on suuruus (pituus) vektorin a
|b| on suuruus (pituus) vektorin b
θ on kulma a ja b välillä
Niin me kerrotaan pituus kertaa pituus b, sitten kerrotaan kosini kulma a ja b välillä
TAI, voimme laskea sen näin:
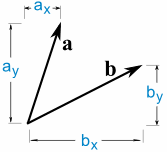
a · b = ax x bx + ay × mennessä
Niin me kerrotaan x: n, moninkertaistaa y: n, sitten lisää.,
Molemmat menetelmät toimivat!
ja tuloksena on luku (kutsutaan ”skalaariksi”, joten tiedämme, ettei se ole vektori).
Huomaa: voit käyttää Vektorikalsulatortoa apunasi.
Miksi cos(θ) ?
OK, kahden vektorin moninkertaistamiseksi on järkevää kertoa niiden pituudet yhdessä, mutta vain silloin, kun ne osoittavat samaan suuntaan.,
Joten me tehdä yksi ”kohta samaan suuntaan” kuin muut kertomalla cos(θ):
 |
 |
|
| Otamme komponentti , joka sijaitsee rinnalla b |
Kuin loistava valo nähdä, jossa varjo sijaitsee |
SITTEN me kerrotaan !,
Oikeassa Kulmassa
Kun kaksi vektoria ovat kohtisuorassa toisiaan pistetulo on nolla.
tämä voi olla kätevä tapa selvittää, ovatko kaksi vektoria suorassa kulmassa.
Kolme tai Enemmän Ulottuvuuksia
Tämä kaikki toimii hyvin 3 (tai enemmän) mitat, liian.
ja voi olla todella hyödyllinen!
kokeilin tuollaista laskentaa kerran, mutta työstin kaikki kulmissa ja etäisyyksissä … se oli hyvin vaikeaa, siihen liittyi paljon trigonometriaa ja aivoihini sattui. Edellä oleva menetelmä on paljon helpompi.,
Cross-Tuote
Dot Tuote antaa skalaari (tavallinen numero) vastaus, ja on joskus kutsutaan skalaari tuote.
mutta on myös Ristituote, joka antaa vektorin vastaukseksi, ja sitä kutsutaan joskus vektorituotteeksi.

















Vastaa