Näytä Mobile Ilmoitus Näytä Kaikki Toteaa, Piilottaa Kaikki Muistiinpanot
osa 3-1 : Parametriset Yhtälöt ja Käyrät
tässä vaiheessa (sekä Calculus ja Calculus II) olemme etsineet lähes yksinomaan toimintoja muodossa \(y = f\left( x \right)\) tai \(x = s\left( y \right)\) ja lähes kaikki kaavat, jotka olemme kehittäneet edellyttävät, että toimintoja voidaan yhdessä nämä kaksi muotoa. Ongelma on se, että kaikki käyrät tai yhtälöt, joita haluaisimme tarkastella, eivät putoa helposti tähän muotoon.
Otetaan esimerkiksi, ympyrä. On helppo kirjoittaa yhtälö ympyrän keskitetty alkuperä säde \(r\).,
\
kuitenkaan emme koskaan pysty kirjoittamaan ympyrän yhtälöä alas yhtenä yhtälönä kummassakaan edellä mainitussa muodossa. Toki voimme ratkaista \(x\) tai \(y\), koska seuraavat kaksi kaavaa osoittavat
\
, mutta itse asiassa jokaisessa näistä on kaksi funktiota. Jokainen kaava antaa osan ympyrän.
\
valitettavasti me yleensä työstämme koko ympyrää, tai yksinkertaisesti emme voi sanoa, että työskentelemme vain yhden osan siitä. Vaikka voimme rajata asiat vain yhteen näistä osista toiminto on silti usein melko epämiellyttävä työskennellä.,
\
Tämä kolmas muuttuja merkitään yleensä \(t\) (kuten teimme täällä), mutta ei tarvitse tietenkään olla. Joskus me rajoittaa arvot \(t\), että käytämme ja toisinaan emme. Tämä on usein riippuvainen ongelma ja vain sen, mitä yritämme tehdä.
auttaa visualisoimaan juuri sitä, mitä parametrinen käyrä on teeskennellä, että meillä on iso vesisäiliö, joka on jatkuvassa liikkeessä ja pudotamme pingispallon säiliöön., Pisteen \(\left( {x,y} \right) = \left( {f\left( t \right),g\left( t \right)} \right)\) on sitten edustavat sijainti ping pong pallo säiliö aika \(t\) ja parametrinen käyrä on jälkeäkään kaikki paikat ping-pong pallo. Huomaa, että tämä ei ole aina oikea analogia, mutta on hyödyllistä aluksi auttaa visualisoimaan, mitä parametrinen käyrä on.
parametrisen käyrän luonnostelu ei ole aina helppoa. Katsotaanpa esimerkki nähdä yksi tapa hahmotella parametrinen käyrä., Tämä esimerkki valaisee myös sitä, miksi tämä menetelmä ei yleensä ole paras.
tässä vaiheessa ainoa vaihtoehto luonnosteluun parametrinen käyrä on valita arvoja \(t\), kytke ne parametriset yhtälöt, ja sitten tontti pistettä. Joten, let ’ s plug in some \(t\)’s.,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Valitettavasti tähän kysymykseen ei ole tässä vaiheessa todellista vastausta. Me yksinkertaisesti valita \(t\): n, kunnes olemme melko varmoja, että meillä on hyvä käsitys siitä, mitä käyrä näyttää. Juuri tämä ongelma poiminta ”hyvä” arvot \(t\), jotka tekevät tämän menetelmän luonnostelu parametriset käyrät yksi köyhempiä valintoja. Joskus meillä ei ole vaihtoehtoja, mutta jos meillä on vaihtoehtoja, meidän pitäisi välttää sitä.
keskustelemme myöhemmissä esimerkeissä vaihtoehtoisesta grafiikkamenetelmästä, joka auttaa selittämään, miten nämä \(t\) arvot valittiin.,
meillä on vielä yksi idea keskusteltavana ennen kuin oikeastaan hahmotamme käyrän. Parametrisilla käyrillä on liikesuunta. Liikesuunta annetaan lisäämällä \(t\). Joten, kun suunnittelet parametriset käyrät, me myös nuolia, jotka osoittavat suuntaan liikkeen. Olemme usein antaa arvoa \(t\), joka antoi erityisiä kohtia kuvaaja sekä tehdä selväksi, arvo \(t\), joka antoi, että erityisesti kohta.
tässä on tämän parametrisen käyrän luonnos.
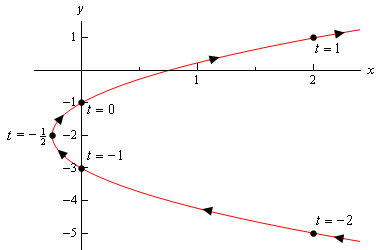
näyttää siltä, että meillä on paraabeli, joka aukeaa oikealle.,
ennen kuin lopetamme tämän esimerkin, on jokseenkin tärkeä ja hienovarainen kohta, josta meidän on ensin keskusteltava. Huomaa, että teimme varma, että myös osa luonnos oikealla pistettä, joka vastaa \(t = – 2\) ja \(t = 1\) osoita, että on olemassa osia luonnos siellä. Jos olisimme yksinkertaisesti pysäytetty luonnos niissä kohdissa olemme osoittaa, että ei ollut osa käyrä oikealle näistä kohdista ja on selvästi. Emme vain laskeneet niitä pisteitä.,
Tämä saattaa tuntua merkityksetön seikka, mutta kuten tulemme näkemään seuraavassa esimerkissä se on tärkeämpää kuin voisi luulla.
Ennen kuin käsitellään paljon helpompi tapa hahmotella tämän kuvaajan katsotaanpa ensin käsitellä rajat parametri. Edellisessä esimerkissä meillä ei ollut rajoituksia parametrille. Ilman parametrin rajoituksia kaavio jatkuu molempiin suuntiin kuten yllä olevassa luonnoksessa esitetään.
parametrilla on kuitenkin usein rajat, ja tämä vaikuttaa parametristen yhtälöiden luonnokseen., Jos haluat nähdä tämän vaikutuksen, katsotaan hieman muunnelma edellisestä esimerkistä.
Huomaa, että ainoa ero täällä on läsnäolo rajat \(t\). Kaikki nämä rajat eivät kerro meille, että emme voi ottaa mitään arvoa \(T\) tämän alueen ulkopuolella. Siksi parametrikäyrä on vain osa edellä olevasta käyrästä. Tässä on parametrinen käyrä tästä esimerkistä.,
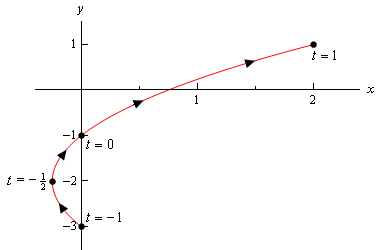
Huomaa, että tämä luonnos me käynnistää ja pysäyttää luonnos oikealla pistettä peräisin päätepisteiden välillä \(t\): n. Tämän vastakohtana on luonnos edellisessä esimerkissä, jossa meillä oli osan luonnos oikealla ”käynnistä” ja ”end” pistettä että me lasketaan.
tässä tapauksessa käyrä alkaa \(t = – 1\) ja päättyy \(t = 1\), kun taas edellisessä esimerkissä käyrä ei oikeastaan aloittaa oikeaan eniten pisteitä, että me lasketaan., Meidän on oltava selvillä luonnoksissamme, jos käyrä alkaa / päättyy oikeaan pisteeseen, tai jos tuo Piste oli yksinkertaisesti ensimmäinen/viimeinen, jonka laskimme.
nyt on aika katsoa helpompi tapa luonnosteluun tämä parametrinen käyrä. Tämä menetelmä käyttää siihen, että monissa, mutta ei kaikissa tapauksissa emme voi oikeastaan poistaa parametri parametriset yhtälöt ja saada toiminto, johon vain \(x\) – ja \(y\). Me joskus soittaa tämän algebrallinen yhtälö erottaa sen alkuperäisestä parametriset yhtälöt., Tässä menetelmässä on kaksi pientä ongelmaa, mutta näihin ongelmiin on helppo puuttua. On tärkeää huomata kuitenkin, että emme aina pysty tähän.
miten poistamme parametrin riippuu parametrisista yhtälöistä, jotka meillä on. Katsotaanpa, miten poistaa parametri joukko parametrinen yhtälöt, että olemme työskennelleet tähän pisteeseen.
parametrikäyrän luonnoksen saaminen poistettuamme parametrin näyttää melko yksinkertaiselta. Meidän tarvitsee vain havainnoida yhtälö, jonka löysimme poistamalla parametri., Kuten jo todettiin, tässä menetelmässä on kuitenkin kaksi pientä ongelmaa. Ensimmäinen on liikesuunta. Yhtälö johon vain \(x\) – ja \(y\) EI anna kulkusuunnassa parametrinen käyrä. Tämä on yleensä helppo ongelma korjata kuitenkin. Katsotaanpa nopeasti johdannaiset parametriset yhtälöt viimeisestä esimerkistä. Ne ovat,
\
Huomaa, että \(x\) johdannainen ei ole niin hyödyllinen tämä analyysi, koska se on sekä positiivisia ja negatiivisia, ja näin ollen \(x\) on sekä lisäämällä ja vähentämällä riippuen arvo \(t\)., Tämä ei auta suuntaan paljon kuin seuraavat käyrä kumpaankaan suuntaan näkyy sekä kasvaa ja vähenee \(x\).
joissakin tapauksissa vain yksi yhtälöistä, kuten tämä esimerkki, antaa suunnan, kun taas toisissa tapauksissa voidaan käyttää jompaakumpaa. On myös mahdollista, että joissakin tapauksissa molempia johdannaisia tarvittaisiin suunnan määrittämiseksi. Se on aina riippuvainen yksittäisten joukko parametriset yhtälöt.,
toinen ongelma parametrin poistamisessa on parhaiten havainnollistettu esimerkissä, sillä törmäämme tähän ongelmaan muissa esimerkeissä.
Okei, se oli todella pitkä esimerkki. Useimmat näistä ongelmista eivät ole niin pitkiä. Meillä oli tässä paljon keskusteltavaa, jotta saimme pari tärkeää ideaa pois alta. Loput esimerkit tässä osiossa ei pitäisi kestää niin kauan käydä läpi.
nyt katsotaan toista esimerkkiä, joka havainnollistaa tärkeää ajatusta parametrisista yhtälöistä.,
niin, näimme kahdessa viimeisessä esimerkissä kaksi parametristen yhtälöiden sarjaa, jotka jollain tavalla antoivat saman kuvaajan. Silti, koska he jäljittivät kaavion eri monta kertaa meidän todella täytyy ajatella niitä eri parametriset käyrät ainakin jollakin tavalla. Tämä saattaa tuntua pieni ero, että meidän ei tarvitse murehtia, mutta kuten näemme myöhemmin osat tämä voi olla erittäin tärkeä ero. Joissakin myöhemmissä osissa tarvitsemme käyrän, joka jäljitetään täsmälleen kerran.,
Ennen kuin siirrymme muita ongelmia, katsotaanpa lyhyesti tunnustaa, mitä tapahtuu muuttamalla \(t\) nt tällaisissa parametriset yhtälöt. Kun olemme tekemisissä parametriset yhtälöt, joissa on vain sinesin ja cosines ja niillä molemmilla on sama argumentti, jos vaihtaa väitettä \(t\) nt, me yksinkertaisesti muuttaa nopeutta, jolla käyrä on jäljittää ulos. Jos \(n > 1\) aiomme lisätä nopeutta ja jos \(n < 1\) meidän tulee vähentää nopeutta.
katsotaan vielä pari esimerkkiä.,
tässä vaiheessa olemme nähneet esimerkkejä siitä, että olisi hahmotella täydellinen kuvaaja, joka meillä on poistamalla parametri, jos otamme riittävän suuri valikoima \(t\): n. Kuitenkin edellisessä esimerkissä olemme nyt nähneet, että tämä ei aina pidä paikkaansa. On enemmän kuin mahdollista saada joukko parametrisia yhtälöitä, jotka jatkuvasti jäljittää vain osan käyrästä. Voimme yleensä määrittää, Jos tämä tapahtuu etsimällä rajoja \(x\) ja \(y\), jotka asetetaan meille parametrinen yhtälö.,
usein käytetään parametrisia yhtälöitä kuvaamaan kappaleen tai hiukkasen polkua. Katsotaanpa esimerkki siitä.
meidän pitäisi antaa pieni varoitus tässä vaiheessa. Koska ideoita mukana niitä olemme keskittyneet parametrinen käyrät selvittää, että osia käyrä useammin kuin kerran. Älä kuitenkaan mene liian syvälle ajatukseen, että näin aina tapahtuu. Monet, ellei useimmat parametriset käyrät vain jäljittää kerran. Ensimmäinen, jota tarkastelimme, on hyvä esimerkki tästä. Tuo parametrinen käyrä ei koskaan toista mitään osaa itsestään.,
tässä jaksossa käsitellään vielä yksi aihe ennen kuin siirrytään eteenpäin. Tähän mennessä olemme aloittaneet parametrisilla yhtälöillä ja poistaneet parametrin parametrin parametrisen käyrän määrittämiseksi.
on kuitenkin aikoja, jolloin haluamme mennä toiseen suuntaan. Kun otetaan huomioon funktio tai yhtälö, voisimme haluta kirjoittaa joukon parametrisia yhtälöitä sille. Näissä tapauksissa sanomme, että parametrisoimme funktion.
Jos otamme Esimerkkejä 4 ja 5 esimerkkeinä voimme tehdä tämän ellipsejä (ja siten piireissä)., Koska ellipsin
\
joukko parametriset yhtälöt olisi,
\
Tämä joukko parametriset yhtälöt jäljittää ulos ellipsin alkaen pisteessä \(\left( {a,0} \right)\) ja jäljittää vastapäivään ja jäljittää tarkalleen, kun välillä \(0 \le t \le 2\pi \). Tämä on melko tärkeä joukko parametrisia yhtälöitä, koska sitä käytetään jatkuvasti joissakin kohteissa, jotka käsittelevät ellipsejä ja / tai ympyröitä.
jokainen käyrä voidaan parametrisoida useammalla kuin yhdellä tavalla. Jokin seuraavista myös parametrisoi saman ellipsin.,
\
\: n(\omega \) läsnäolo muuttaa ellipsin pyörimisnopeutta, kuten näimme esimerkissä 5. Huomaa myös, että kaksi viimeistä jäljittää ellipsejä myötäpäivään suuntaan liikkeen (kannattaa tarkistaa tämä). Huomaa myös, että ne eivät kaikki aloita samasta paikasta(jos ajattelemme \(t = 0\) lähtökohtana, joka on).
ellipsistä on tietysti olemassa paljon muitakin parametrejä, mutta idea syntyy. On tärkeää muistaa, että jokainen parametrointi jäljittää käyrä kerran mahdollisesti eri valikoiman \(t\): n., Jokainen parametrisointi voi kiertää eri liikesuunnilla ja se voi alkaa eri kohdista.
saatat huomata, että sinun tarvitsee parametrointi ellipsi, joka alkaa klo tietyn paikka ja se on tiettyyn suuntaan liikkeen ja niin, nyt tiedämme, että töitä voit kirjoittaa joukko parametriset yhtälöt, jotka antavat sinua käyttäytyminen, että olet jälkeen.
Nyt, katsotaanpa kirjoittaa pari muuta tärkeää parameterizations ja kaikki kommentit liikkeen suuntaa, lähtökohta, ja välillä \(t\): n yhden trace (tarvittaessa) ovat edelleen totta.,
Ensimmäinen, koska ympyrä ei ole mitään muuta kuin erityinen tapaus ellipsin voimme käyttää parametrointi ellipsin saada parametriset yhtälöt ympyrän keskipisteessä alkuperä säde \(r\) samoin. Yksi mahdollinen tapa parametrisoida ympyrä on,
\ \
tässä vaiheessa se voi tuntua, että kaikki hyödyllistä tehdä parametrointi toiminto, kuten tämä, mutta on monia tapauksia, joissa se on itse asiassa helpompaa, tai se voi jopa olla tarpeen, työskennellä parametrointi sijasta tehtävä itse., Valitettavasti lähes kaikki nämä tapaukset tapahtuvat Calculus III kurssin.
















Vastaa