Näytä Mobile Ilmoitus Näytä Kaikki Toteaa, Piilottaa Kaikki Muistiinpanot
4-11§: Lineaarinen Likiarvoja
tässä osiossa olemme menossa katsomaan sovellus ei johdannaisten mutta tangentin toiminnon. Tietenkin, saada tangentin meidän täytyy ottaa johdannaisia, joten jollain tavalla tämä on sovellus, johdannaisten sekä.
\
vilkaise funktion ja sen tangenttiviivan seuraavaa kuvaajaa.
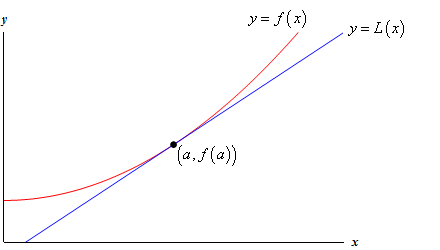
Niin, miksi teemme tätä? Katsotaanpa esimerkkiä.,
lineaariset approksimaatiot tekevät erittäin hyvää työtä \(F\left( x \right)\) arvojen lähentämisessä, kunhan pysymme ”lähellä” \(x = a\). Kuitenkin, kauempana \(x = a\) saamme huonompi approksimaatio on todennäköisesti. Suurin ongelma tässä on se, että kuinka lähellä meidän täytyy pysyä \(x = a\), jotta voidaan saada hyvä lähentämisestä riippuu sekä toiminto käytämme ja arvo \(x = a\), että käytät. Usein ei myöskään ole helppoa tapaa ennustaa, kuinka kaukana \(x = a\) voimme saada ja silti on ”hyvä” likiarvo.,
katsotaanpa toista esimerkkiä, jota käytetään paikoin melko paljon.
Tämä on itse asiassa jokseenkin tärkeä lineaarinen approksimaatio. Optiikassa tätä lineaarista approksimaatiota käytetään usein kaavojen yksinkertaistamiseen. Tätä lineaarista approksimaatiota käytetään myös kuvaamaan heilurin liikettä ja värähtelyä jonossa.
















Vastaa