
Tänään tarkastelemme suosituimmista vaihtoehdoista hinnoittelu malli. Musta Scholes-Malli, joka tunnetaan myös nimellä Black-Scholes-Merton-menetelmä on matemaattinen malli hinnoittelu, sopimukset. Se toimii arvioimalla rahoitusinstrumenttien vaihtelua. Tekniikka perustuu oletukseen, että hinnat noudattavat lognormaalista jakautumista. Tämän perusteella se saa option arvon.,
– Se sopii paremmin polku-riippumaton vaihtoehtoja, joista sijoittajat eivät voi käyttää ennen niiden eräpäivää. Tämä tekee siitä erilaisen kuin Binominen Optiohinnoittelumalli, joka on riskineutraali menetelmä polkusta riippuvien vaihtoehtojen (esim.
Analyytikot ja sijoittajat pitävät Black Scholes-mallin yksi keskeisiä käsitteitä nykyaikaisen taloushallinnon teoriaa.
Käyttöön vuonna 1973 Journal of political Economy, jonka Fischer Black ja Myron Scholes, ja myöhemmin rakennettu Robert Merton-malli voitti Nobelin taloustieteen vuonna 1997.,
malli noudattaa differentiaaliyhtälöä, jonka avulla ratkomme optioiden hintoja. Käytämme mallin vakiovaihtelua eurooppalaisiin tyylivaihtoehtoihin. Musta Scholes ei sovellu Amerikkalainen tyyli vaihtoehtoja, koska se ei pidä sijoittajat voivat käyttää näitä asetuksia milloin tahansa ennen niiden viimeistä käyttöpäivää.
menetelmä olettaa, hinta kohde-etuutena olevan osakkeen seuraa lognormaalina jakelu, koska se ei voi olla negatiivinen. Jakelu malli perustuu perustuu Brownin liike, teoria ennustaa luonnossa esiintyviä satunnaisia ilmiöitä.,
käytämme malli laskea arvio vaihtoehto on hinta, käyttäen seuraavat tiedot:
- nykyinen hinta;
- lunastushinta;
- Aikaa kulunut;
- Odotettu osinkotuotto;
- Odotettavissa korko; ja
- Odotettavissa oleva volatiliteetti.
aluksi mallissa ei huomioida osingonmaksun vaikutusta. Siksi se on usein mukautettu tehdä niin määrittämällä Ex-osinko päivämäärä arvo kohde-etuutena., Osinkotuotto on vähentää nykyinen osakekurssi koska vaihtoehto haltija luopuu osingot.
oletukset
Black Scholesin malli toimii vain, jos teemme tiettyjä oletuksia.,s esiintyä vaihtoehto elinkaari (tämä oli oletus, että alkuperäinen malli, joka analyytikot ovat sittemmin poistanut lisäämällä osinkotuotto malli kaava);
Black Scholes-Kaava
malli, kaava on matemaattisesti melko monimutkainen, joka ei ole erityinen ongelma, koska emme voi palkata erikoistuneita työkaluja laskea se meille. Silti on tärkeää ymmärtää, miten se toimii.,
laskea hinta puhelun vaihtoehto, alla Musta Scholes-malli, voimme käyttää seuraavaa yhtälöä:
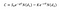
Missä:
- S0 on varastossa hinta;
- e on eksponentiaalinen määrä;
- q on osinkotuotto prosentteina;
- T on aikavälin (yksi vuosi tulee olla T=1, kun kuusi kuukautta on T=0.,5);
- N(d1) on delta puhelun vaihtoehto, eli muuttaa puhelun hinta yli vaihto osakekurssi;
- K on toteutushinta;
- r on riskitön korko; ja
- N(d2) on todennäköisyys, että tulevaisuudessa osakekurssi on korkeampi kuin lunastushinta, todennäköisyys, me osoitamme vaihtoehto.
toisella puolella on osakkeen hinta kerrottuna kumulatiivinen normaali jakelu d1, ja muut — lakko hinta, diskontattu aika T ja sitten kerrottuna kumulatiivinen normaali jakelu d2.,
Missä voimme laskea d1 ja d2 seuraavat kaavat:
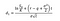
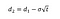
Missä σ on volatiliteetti tuotto kohde-etuuden.,
Voimme soveltaa samaa logiikkaa laittaa vaihtoehto:

Liity uutiskirjeemme ILMAINEN Excel Benchmark Analysis Template
Esimerkki Musta Scholes Laskelma
paremmin havainnollistaa käsitteen takana Musta Scholes-Malli, otamme katso seuraava malli. Aloitamme mallipanoksilla., Kuten edellä mainittiin, tarvitsemme seuraavat kuusi muuttujaa laskea puhelun ja laittaa vaihtoehto arvot.

Seuraavaksi laskemme asetukset’ – parametrit. Alkaen d1, saamme 0,39 meidän malli oletukset.

laskea sitä, emme yksinkertaisesti siirtää kaava d1 Excel.,
Following the same approach, we calculate d2, N(d1) and N(d2).

With those, we can calculate the Call Option Price and the Put Option Price.,

Voimme käyttää Soita-Laita Pariteetti sääntö tarkistaa, onko meidän kaavat ja laskelmat ovat oikein.

Nyt meillä on malli laskea Puhelun ja Laittaa vaihtoehtoja, hinnat, voimme mennä pidemmälle ja tarkastella, miten eri parametreista vaikuttavat tuloksiin meidän malli., Data Table toiminnallisuus Excel on hyvä työkalu valmistella joitakin herkkyys analyysi taulukoita meidän muuttujia. Voit oppia käyttämään Datataulukoita herkkyysanalyysin artikkelissamme.
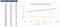
katsotaan osakekurssia, jos se muuttuu 10 eurosta 100 euroon ja miten se vaikuttaa puheluun ja laittaa arvot. Huomaamme, että osto-optiolla ei ole arvoa ennen kuin osakekurssi osuu 40 euroon. Put-optiolle nähdään kääntöpuoli, jossa sen arvo osuu nollaan, kun osakekurssi menee yli 85 euron.,

Jos valmistaudumme sama herkkyys taulukon Lakko Hinta, voimme tarkkailla käänteinen suhde. Kun lakon hinta nousee, puhelun arvo laskee ja myyntiarvo nousee.

katsotaanpa myös katsomaan riski-ilmainen tahtiin., Kun se kasvaa, tämä myös lisää vaadittua tuottoprosenttia. Tämän jälkeen tämä laskee varastojen arvoa. Huomaamme suoran suhteen, kun riskitön korko kasvaa, myös osto-Option arvo nousee, kun taas Put-Option arvo laskee arvoaan.
Seuraavat samaa lähestymistapaa, voit mennä eteenpäin ja katso loput parametrit ja miten ne vaikuttavat Vaihtoehto Arvot., Voit ladata Excel-mallin artikkelin lopussa ja käydä läpi herkkyysanalyysin siellä.
Esimerkkimallin voi ladata Excelistä alkuperäisestä artikkelista.
Johtopäätös
on tärkeää muistaa, että Black-Scholes-Merton-malli on teoreettinen käsite. Yritämme sen avulla arvioida markkinoiden käyttäytymistä. Kun käytämme tuloksia päätöksentekoprosessissamme, meidän on kuitenkin ymmärrettävä mallin perusoletukset ja se, miten se poikkeaa todellisuudesta.,
kaava auttoi optiokauppaa tulemaan suositummaksi, koska se saa sen näyttämään vähemmän uhkapeliltä. Nykyään Black Scholesin erilaiset muunnokset ovat laajalti suosittuja riskinhallinnan perusstrategioina, jotka liittyvät volatiliteettiin.
voit osoittaa tukeasi jakamalla artikkelin kollegoiden ja ystävien kanssa.
















Vastaa