Un vector que tiene magnitud (¿cuánto es) y dirección:
Aquí hay dos vectores:

pueden ser multiplicadas mediante el «Producto escalar» (véase también el Producto Cruzado).,
se puede calcular el Producto escalar de dos vectores de esta manera:

a · b = |a| x |b| × cos(θ)
Donde:
|a| es la magnitud (longitud) de un vector
|b| es la magnitud (longitud) del vector b
θ es el ángulo entre a y b
Así que multiplicamos la longitud de las veces la longitud de b, luego se multiplica por el coseno del ángulo entre a y b
O se puede calcular de esta manera:
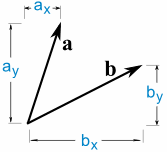
a · b = ax × bx + ay ×
por Lo que se multiplican las x, multiplicar el y, a continuación, en agregar.,
Ambos métodos funcionan!
Y el resultado es un número (llamado «escalar» por lo que sabemos que no es un vector).
Nota: puede utilizar el vector Calculatorpara ayudarle.
¿por qué cos (θ) ?
OK, para multiplicar dos vectores tiene sentido multiplicar sus longitudes juntas pero solo cuando apuntan en la misma dirección.,
por Lo tanto, hacer una «apuntan en la misma dirección» como la otra multiplicando por cos(θ):
 |
 |
|
| Tomamos el componente de un que se encuentra junto a b |
Como el resplandor de una luz para ver cuando la sombra se encuentra |
a CONTINUACIÓN, multiplicamos !,
ángulos rectos
Cuando dos vectores están en ángulos rectos entre sí, el producto escalar es cero.
esta puede ser una manera práctica de averiguar si dos vectores están en ángulos rectos.
Tres o Más Dimensiones
todo Esto funciona bien en 3 (o más) dimensiones, demasiado.
y en realidad puede ser muy útil!
probé un cálculo como ese Una vez, pero trabajé todo en ángulos y distancias … fue muy difícil, involucró mucha trigonometría, y me dolió el cerebro. El método anterior es mucho más fácil.,
producto cruzado
El producto escalar da una respuesta escalar (número ordinario), y a veces se llama el producto escalar.
pero también está el producto cruzado que da un vector como respuesta, y a veces se llama el producto vectorial.

















Deja una respuesta