probabilidad para rodar dos dados con los puntos de seis lados como 1, 2, 3, 4, 5 y 6 puntos en cada dado.

cuando se lanzan dos dados simultáneamente, por lo tanto el número de evento puede ser 62 = 36 porque cada dado tiene 1 a 6 números en sus caras. Luego, los posibles resultados se muestran en la siguiente tabla.,
Probabilidad espacio Muestral para dos dados (resultados):
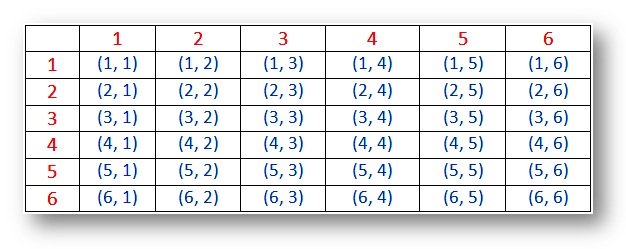
Nota:
(i) Los resultados (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) y (6, 6) son llamados dobletes.
(ii) el par (1, 2) y (2, 1) son resultados diferentes.
Problemas resueltos que implican probabilidad de tirar dos dados:
1. Se lanzan dos dados. Sea A, B, C los eventos de obtener una suma de 2, una suma de 3 y una suma de 4 respectivamente., A continuación, muestran que
(i) a es un evento simple
(ii) B y C son eventos compuestos
(iii) a y B son mutuamente excluyentes
Solución:
Claramente, tenemos
A = {(1, 1)}, B = {(1, 2), (2, 1)} y C = {(1, 3), (3, 1), (2, 2)}.
(i) dado que A consiste en un único punto de muestra, es un evento simple.
(ii) dado que tanto B como C contienen más de un punto de muestra, cada uno de ellos es un evento compuesto.
(iii) dado que A B B = ∅, A y B son mutuamente excluyentes.
2. Se lanzan dos dados., A es el evento que la suma de los números mostrados en los dos dados es 5, y B es el evento que al menos uno de los dados muestra un 3. ¿son los dos eventos (I) mutuamente excluyentes, (ii) exhaustivos? Dé argumentos en apoyo de su respuesta.
Solución:
Cuando se tiran dos dados, tenemos n(S) = (6 × 6) = 36.
Ahora, Un = {(1, 4), (2, 3), (4, 1), (3, 2)}, y
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.
Por lo tanto, A y B no son mutuamente excluyentes.,
(ii) también, a A B ≠ S.
por lo tanto, a y B no son eventos exhaustivos.
Más ejemplos relacionados con las preguntas sobre las probabilidades de lanzar dos dados.
3. Dos dados son lanzados simultáneamente.,) consiguiendo un doblete
(v) obtener una suma de 8
(vi) obtener la suma divisible por 5
(vii) obtener la suma de al menos 11
(viii) obtener un múltiplo de 3 como la suma
(ix) obtener un total de al menos 10
(x) obtener un número como la suma
(xi) obtener un número primo como la suma
(xii) consiguiendo un doblete de números
(xiii) obtener un múltiplo de 2 en un dado y un múltiplo de 3 en el otro morir
Solución:
Dos diferentes dados son lanzados simultáneamente ser la número 1, 2, 3, 4, 5 y 6 en sus rostros., Sabemos que en un solo lanzamiento de dos dados diferentes, el número total de posibles resultados es (6 × 6) = 36.
(i) obtener seis como producto:
Let E1 = evento de obtener seis como producto. El número cuyo producto es seis será E1 = = 4
Por lo tanto, probabilidad de obtener ‘seis como producto’
número de resultados favorables
P(E1) = número Total de resultados posibles
= 4/36
= 1/9
(ii) obtener suma ≤ 3:
sea E2 = evento de obtener suma ≤ 3., El número cuya suma ≤ 3 será E2 = = 3
Por lo tanto, probabilidad de obtener ‘suma ≤ 3’
número de resultados favorables
P(E2) = número Total de resultados posibles
= 3/36
= 1/12
(iii) obtener suma ≤ 10:
sea E3 = evento de obtener suma ≤ 10. El número cuya suma ≤ 10 será E3 =
= 33
Por lo tanto, probabilidad de obtener ‘suma ≤ 10’
número de resultados favorables
P(E3)= número Total de resultados posibles
= 33/36
= 11/12
(iv)obtener un doblete:sea E4 = evento de obtener un doblete., El número que doblete será E4 = = 6
Por lo tanto, probabilidad de colocar ‘un doblete’
número de resultados favorables
P(E4) = número Total de resultados posibles
= 6/36
= 1/6
(v)obtener una suma de 8:
Let E5 = evento de obtener una suma de 8. El número que es una suma de 8 será E5 = = 5
Por lo tanto, probabilidad de obtener ‘una suma de 8’
número de resultados favorables
P(E5) = número Total de resultados posibles
= 5/36
(vi)obtener suma divisible por 5:
Let E6 = evento de obtener suma divisible por 5., El número cuya suma divisible por 5 será E6 = = 7
Por lo tanto, probabilidad de obtener ‘suma divisible por 5’
número de resultados favorables
P(E6) = número Total de resultados posibles
= 7/36
(vii)obtener la suma de atleast 11:
Let E7 = evento de obtener la suma de atleast 11. Los eventos de la suma de atleast 11 serán E7 = = 3
Por lo tanto, probabilidad de obtener ‘suma de atleast 11’
número de resultados favorables
P(E7) = número Total de resultados posibles
= 3/36
= 1/12
(viii) obteniendo un Multiple de 3 como la suma:
sea E8 = evento de obtener un múltiplo de 3 como la suma., Los eventos de un múltiplo de 3 como suma serán E8 = = 12
Por lo tanto, probabilidad de obtener ‘un múltiplo de 3 como suma’
número de resultados favorables
P(E8) = número Total de resultados posibles
= 12/36
= 1/3
(ix) obteniendo un total de al menos 10:
Let E9 = evento de obtener un total de al menos 10., Los eventos de un total de atleast 10 serán E9 = = 6
Por lo tanto, probabilidad de obtener ‘un total de atleast 10’
número de resultados favorables
P(E9) = número Total de resultados posibles
= 6/36
= 1/6
(x) obtener un evennumber como la suma:
Let E10 = evento de obtener un número par como la suma., Los eventos de un número par como la suma serán E10 = = 18
Por lo tanto, probabilidad de colocar ‘un número par como la suma
número de resultados favorables
P(E10) = número Total de resultados posibles
= 18/36
= 1/2
(xi) obtener un primenumber como la suma:
Let E11 = evento de obtener un número primo como la suma., Los eventos de un número primo como la suma serán E11 = = 15
Por lo tanto, probabilidad de obtener ‘un número primo como la suma’
número de resultados favorables
P(E11) = número Total de resultados posibles
= 15/36
= 5/12
(xii) Obtener un doblete de números pares:
sea E12 = evento de obtener un doblete de números pares., Los eventos de un doblete de números pares serán E12 = = 3
Por lo tanto, la probabilidad de obtener ‘un doblete de números pares’
número de resultados favorables
P(E12) = número Total de resultados posibles
= 3/36
= 1/12
(xiii) obtener un múltiplo de 2 en un dado y un múltiplo de 3 en el otro dado:
Let E13 = evento de obtener un múltiplo de de 2 en un dado y un múltiplo de 3 en el otro dado., Los eventos de un múltiplo de 2 en un dado y un múltiplo de 3 en el otro dado serán E13 = = 11
Por lo tanto, probabilidad de obtener ‘un múltiplo de 2 en un dado y un múltiplo de 3 en el otro dado’
número de resultados favorables
P(E13) = número Total de posibles resultados
= 11/36
4. Se lanzan dos unidades. Encuentre (i) las probabilidades a favor de obtener la suma 5, y (ii) theodds en contra de obtener la suma 6.
solución:
sabemos que en un solo lanzamiento de dos dados, el número total de posibles resultados es (6 × 6) = 36.
Sea S el espacio de muestra. Entonces, n ( S) = 36.,
(i) las probabilidades a favor de obtener la suma 5:
sea E1 el evento de obtener la suma 5. Entonces,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P(E1) = 4
por lo Tanto, P(E1) = n(E1)/n(S) = 4/36 = 1/9
⇒ probabilidades en favor de E1 = P(E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii) las probabilidades en contra de obtener la suma 6:
sea E2 el evento de obtener la suma 6. Entonces,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P(E2) = 5
por lo Tanto, P(E2) = n(E2)/n(S) = 5/36
⇒ probabilidades en contra E2 = /P(E2) = (1 – 5/36)/(5/36) = 31/5.
5., Dos dados, uno azul y otro naranja, se lanzan simultáneamente. Encuentra la probabilidad de obtener
(i) números iguales en ambos
(ii) dos números que aparecen en ellos cuya suma es 9.,
Solución:
Los resultados posibles son:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
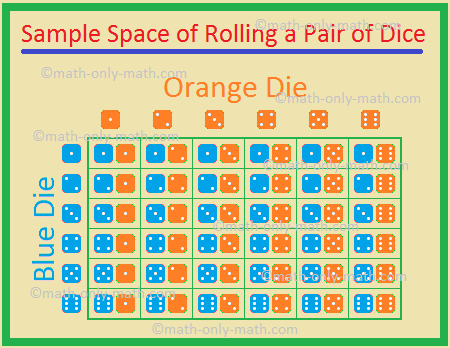
por lo Tanto, el número total de resultados posibles = 36.,
(i) número de resultados favorables para el evento E
= número de resultados que tienen números iguales en ambos dados
= 6 .
Así que, por definición, P(E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) Número de resultados favorables del evento F
= Número de resultados en los que dos números que aparecen en ellos tiene la suma 9
= 4 .
así, por definición, P (F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
estos ejemplos nos ayudarán a resolver diferentes tipos de problemas basados en la probabilidad de lanzar dos dados.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Deja una respuesta