ir a área de superficie o volumen.
Un prisma es un objeto sólido con:
- idénticos termina
- las caras planas
- y la misma sección transversal a lo largo de su longitud !
una sección transversal es la forma hecha cortando directamente a través de un objeto.
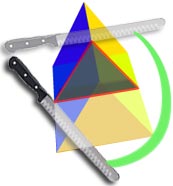
La sección transversal de este objeto es un triángulo …
.. tiene la misma sección transversal a lo largo de su longitud …
… así que es un prisma triangular.,
|
intente dibujar una forma en un pedazo de luego imagine que se extiende hacia arriba desde la hoja de papel … |
 |
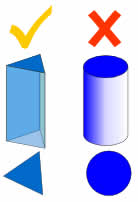
No hay Curvas!
un prisma es un poliedro, lo que significa que todas las caras son planas!
sin lados curvos.
Por ejemplo, un cilindro no es un prisma, porque tiene lados curvos.,
Bases
Los extremos de un prisma son paralelos
y cada uno se llama una base.
Lados
Las caras laterales de un prisma son paralelogramos
(4 caras, figuras con lados opuestos paralelos)
Estos son todos los Prismas:
y más!

Ejemplo: Este hexagonal de los cristales de hielo.
Se parece a un hexágono, pero debido a que tiene algún grosor, ¡en realidad es un prisma hexagonal!
fotografía de la NASA / Alexey Kljatov.,
prismas regulares vs irregulares
todos los ejemplos anteriores son prismas regulares, porque la sección transversal es regular (en otras palabras, es una forma con longitudes de borde iguales y ángulos iguales.,)
Here is an example of an Irregular Prism:
| Irregular Pentagonal Prism: | ||
 |
 |
|
| Cross-Section | ||
| It is «irregular» because the cross-section is not «regular» in shape.,div> área de superficie = 2 × Área de Base
+ perímetro de Base × Longitud ejemplo: Cuál es el área de superficie de un prisma donde el área de base es 25 m2, el perímetro de base es 24 m y la longitud es 12 m: Área = 2 × área base + perímetro base × longitud
= 2 × 25 m2 + 24 m × 12 m
= 50 m2 + 288 m2
= 338 m2
(Nota: tenemos una herramienta de cálculo de área) volumen de un prismade uno de los tiempos finales de la longitud del prisma., Volumen = Área de la Base × Longitud Ejemplo: ¿Cuál es el volumen de un prisma donde el área de la base es de 25 m2 y que es de 12 m de largo: Volumen = Área × Longitud
= 25 m2 × 12 m
= 300 m3
Jugar con él aquí., La fórmula también funciona cuando se «inclina» (oblicuo), pero recuerde que la altura es perpendicular a la base: Y este es el por qué:
© 2021 Tombouctou Tema por Anders Noren — Arriba ↑ | ||






















Deja una respuesta