Hoy echamos un vistazo a las opciones más populares, modelo de fijación de precios. El modelo Black Scholes, también conocido como el método Black-Scholes-Merton, es un modelo matemático para los contratos de opciones de precios. Funciona mediante la estimación de la variación en los instrumentos financieros. La técnica se basa en el supuesto de que los precios siguen una distribución lognormal. Basado en esto, deriva el valor de una opción.,

es más adecuado para opciones independientes de la trayectoria, que los inversores no pueden ejercer antes de su fecha de vencimiento. Esto lo hace diferente del modelo Binomial de precios de opciones, que es un método neutral de riesgo para valorar opciones dependientes de la ruta (por ejemplo, opciones estadounidenses).

Los analistas e inversores consideran que Black Scholes es uno de los conceptos esenciales en la teoría financiera moderna.

introducido en 1973 en el Journal of Political Economy, por Fischer Black y Myron Scholes, y posteriormente construido por Robert Merton, el modelo ganó el Premio Nobel de Economía en 1997.,

el modelo sigue una ecuación diferencial, que utilizamos para resolver los precios de las opciones. Utilizamos la variación estándar del modelo para las opciones de estilo europeo. Black Scholes no es adecuado para opciones de estilo americano, ya que no considera que los inversores puedan ejercer estas opciones en cualquier momento antes de su fecha de vencimiento.

el método asume que el precio de la acción subyacente sigue una distribución lognormal, ya que no puede ser negativo. La distribución en la que se basa el modelo se basa en el movimiento browniano, una teoría para predecir fenómenos aleatorios que ocurren naturalmente.,

utilizamos el modelo para calcular una estimación del precio de una opción, utilizando la siguiente información:

  • El precio actual;
  • El precio de ejercicio;
  • Tiempo de vencimiento;
  • rendimiento esperado de dividendos;
  • tasa de interés esperada; y
  • volatilidad esperada.

inicialmente, el modelo no considera el efecto de los pagos de dividendos. Por lo tanto, con frecuencia se adapta para hacerlo determinando el valor de fecha ex-dividendo del activo subyacente., El rendimiento del dividendo tiene el efecto de reducir el precio actual de las acciones porque el titular de la opción renuncia a los dividendos.

suposiciones

El modelo de Black Scholes solo funciona si hacemos ciertas suposiciones.,los mercados son completamente eficientes, lo que significa que no podemos predecir sus movimientos;

  • Las opciones de compra y venta no implican costos de transacción;
  • tanto la volatilidad del activo subyacente como la tasa libre de riesgo permanecen constantes hasta la fecha de vencimiento, lo que no es correcto, ya que en realidad la volatilidad cambia con la oferta y la demanda; y
  • los rendimientos del activo subyacente siga una distribución normal.,

    • fórmula de Black Scholes

    la fórmula del modelo es bastante compleja matemáticamente, lo cual no es un problema en particular, ya que podemos emplear herramientas especializadas para calcularla por nosotros. Pero sigue siendo esencial entender cómo funciona.,

    Para calcular el precio de una opción call, bajo el Black Scholes modelo, podemos utilizar la siguiente ecuación:

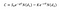
    Donde:

    • S0 es el precio de las acciones;
    • e es el número exponencial;
    • q es el rendimiento de los dividendos porcentaje;
    • T es el plazo (un año será T=1, mientras que los seis meses será T=0.,5);
    • N(d1) es el delta de la opción call, lo que significa el cambio en el precio de la llamada durante el cambio en el precio de las acciones;
    • K es el precio de ejercicio;
    • r es la tasa libre de riesgo; y
    • N(d2) es la probabilidad de que el precio futuro de las acciones sea mayor que el precio de ejercicio, la probabilidad de que ejerceremos la opción.

    Un lado es el precio de las acciones multiplicado por la distribución normal estándar acumulada de d1, y el otro — el precio de ejercicio, descontado al tiempo T y luego multiplicado por la distribución normal estándar acumulada de d2.,

    Donde podemos calcular d1 y d2 con las siguientes fórmulas:

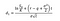
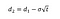
    Donde σ es la volatilidad de los retornos del activo subyacente.,

    podemos aplicar la misma lógica para una opción put:

    Únase a nuestro Boletín de noticias para un Excel LIBRE de Análisis de Referencia de la Plantilla

    Ejemplo de Black Scholes Cálculo

    Para ilustrar mejor el concepto detrás de la Black Scholes Modelo, vamos a echar un vistazo en el siguiente modelo. Comenzamos con las entradas del modelo., Como se discutió anteriormente, necesitamos las siguientes seis variables para calcular los valores de las opciones call y put.

    a continuación, vamos a calcular las opciones de parámetros. Comenzando con d1, obtenemos 0.39 de nuestros supuestos modelo.

    calcular, nosotros simplemente la transferencia de la fórmula para la d1 a Excel.,

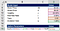
    Following the same approach, we calculate d2, N(d1) and N(d2).

    With those, we can calculate the Call Option Price and the Put Option Price.,

    podemos emplear la Llamada-Poner la Paridad de la regla para comprobar si nuestras fórmulas y cálculos son correctos.

    Ahora que ya tenemos nuestro modelo para calcular las opciones Call y Put precios, podemos ir un paso más allá y ver cómo los diferentes parámetros de entrada afectar los resultados de nuestro modelo., La funcionalidad de tabla de datos en Excel es una gran herramienta para preparar algunas tablas de análisis de sensibilidad para nuestras variables. Puede aprender a usar tablas de datos en nuestro artículo de análisis de sensibilidad.

    veamos el precio de las acciones si cambia de €10 a €100 y cómo afecta a los valores de Call y Put. Notamos que la opción Call no tiene valor hasta que el precio de las acciones alcanza los 40€. Vemos lo contrario para la opción Put, donde su valor llega a cero una vez que el precio de las acciones supera los €85.,

    Si nos preparamos de la misma sensibilidad para la tabla de Precio de ejercicio, se puede observar la relación inversa. A medida que aumenta el precio de ejercicio, el valor de llamada baja y el valor de Venta sube.

    también Vamos a echar un vistazo a los riesgos tasa libre., A medida que aumenta, esto también aumenta la tasa de rendimiento requerida. Posteriormente, esto disminuye el valor de las existencias. Notamos una relación directa, a medida que aumenta la tasa libre de riesgo, también aumenta el valor de la opción de compra, mientras que el valor de la opción de Venta disminuye su valor.

    Siguiendo el mismo enfoque, usted puede seguir adelante y mirar el resto de los parámetros y cómo afectan a los Valores de Opción., Puede descargar el modelo de Excel al final del artículo y repasar el análisis de sensibilidad allí.

    Puede descargar el modelo de ejemplo en Excel en el artículo original.

    conclusión

    es importante recordar que el modelo Black-Scholes-Merton es un concepto teórico. Lo usamos para tratar de estimar el comportamiento del mercado. Sin embargo, cuando utilizamos los resultados en nuestro proceso de toma de decisiones, tenemos que entender las suposiciones subyacentes en el modelo y cómo se desvía de la realidad.,

    la fórmula ayudó a que el comercio de opciones se volviera más popular, ya que hace que se parezca menos a los juegos de azar. Hoy en día, varias modificaciones de Black Scholes son ampliamente populares como estrategias fundamentales para el control de riesgos, asociadas con la volatilidad.

    Puede mostrar su apoyo compartiendo el artículo con colegas y amigos.