Compartir en

Contenido (hacer Clic para saltar a la sección):

  1. Todo sobre el…
    • Media
    • Modo
    • Mediana
  2. ¿Cómo encontrar la media, la mediana y el modo de mano.
  3. encuentra la media, mediana y modo con la tecnología:
    • SPSS
    • TI83

Overview

Stuck on how to find the mean, median, & mode in statistics?,

  1. La media es el promedio de un conjunto de datos.
  2. el modo es El número más común en un conjunto de datos.
  3. La mediana es el centro del conjunto de números.

de los tres, la media es la única que requiere una fórmula. Me gusta pensar en ello en el otro sentido del diccionario de la palabra (como en, es media en lugar de agradable!). Eso es porque, en comparación con los otros dos, no es tan fácil trabajar con él.,


Consejos para recordar la diferencia

tiene problemas para recordar la diferencia entre la media, mediana y moda? Aquí hay un par de consejos que pueden ayudar. También puede consultar a los tutores en Chegg.com (¡tus primeros 30 minutos son GRATIS!).

  • » a la mode » es una palabra francesa que significa moda ; también se refiere a una forma popular de servir helado. Así que «el régimen» es el miembro más popular o a la moda de la multitud de números. El modo de palabras también es como la mayoría.,
  • La» Media «requiere que hagas aritmética (sumando todos los números y dividiendo) para que sea la» media».
  • «Median» tiene el mismo número de letras que «Middle».

¿todavía no está seguro de cuál es la diferencia entre los tres? Vea el video o siga leyendo para obtener más información:

acepte estadísticas, cookies de marketing para ver este video.

La Media

Significa vs Mediana
Significa vs, Promedio
«medias» específicas comúnmente utilizadas en Estadísticas
otros tipos

Media vs mediana

ambos son medidas de dónde se encuentra el Centro de un conjunto de datos (llamado «tendencia Central» en estadísticas), pero generalmente son números diferentes. Por ejemplo, tome esta lista de números: 10, 10, 20, 40, 70.

  • la media (informalmente, el «promedio») se encuentra sumando todos los números juntos y dividiendo por el número de elementos en el conjunto: 10 + 10 + 20 + 40 + 70 / 5 = 30.
  • La mediana se encuentra ordenando el conjunto de Menor a Mayor y encontrando el centro exacto., La mediana es sólo el número medio: 20.

a veces los dos serán el mismo número. Por ejemplo, el conjunto de datos 1, 2, 4, 6, 7 tiene una media de 1 + 2 + 4 + 6 + 7 / 5 = 4 y una mediana (un medio) de 4.

Media vs promedio: ¿Cuál es la diferencia?

cuando empezaste en matemáticas, probablemente te enseñaron que un promedio era una cantidad «media» para un conjunto de números. Usted sumó los números, dividido por el número de elementos que puede y voila! obtienes el promedio. Por ejemplo, el promedio de 10, 5 y 20 es:

10 + 6 + 20 = 36 / 3 = 12.,

usted comenzó a estudiar estadísticas y de repente el «promedio» ahora se llama la media. ¿Qué ha ocurrido? La respuesta es que tienen el mismo significado(son sinónimos).

dicho esto, técnicamente, la palabra media es la abreviatura de la media aritmética. Usamos diferentes palabras en las estadísticas, porque hay múltiples tipos diferentes de medios, y todos hacen cosas diferentes.

«significa» específico que se usa comúnmente en Estadísticas

probablemente te encuentres con estos en tu clase de estadísticas., Tienen significados muy estrechos:

  • media de la distribución muestral: utilizada con distribuciones de probabilidad, especialmente con el teorema del límite Central. Es un promedio de un conjunto de distribuciones.
  • media muestral: el valor medio de una muestra.
  • media de la población: el valor medio en una población.

Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, 1962.

otros tipos

hay otros tipos de medios, y los usarás en varias ramas de las matemáticas., La mayoría tiene aplicaciones muy estrechas para campos como las finanzas o la física; si estás en estadísticas elementales, probablemente no trabajarás con ellas.

Estos son algunos de los tipos más comunes que encontrará.

  1. media Ponderada.
  2. media armónica.
  3. media geométrica.
  4. media aritmética-Geométrica.
  5. raíz-media media cuadrada.
  6. Media Heroniana.
  7. Gráfico de Media

  1. Media Ponderada

    Estos son bastante comunes en las estadísticas, especialmente cuando se estudian poblaciones., En lugar de que cada punto de datos contribuya por igual al promedio final, algunos puntos de datos contribuyen más que otros. Si todos los pesos son iguales, entonces esto será igual a la media aritmética. Hay ciertas circunstancias en las que esto puede dar información incorrecta, como se muestra en la paradoja de Simpson.

  2. la Media Armónica

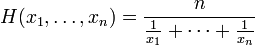
    La fórmula armónica.

    para encontrarlo:

    1. agregue los recíprocos de los números en el conjunto., Para encontrar un recíproco, voltear la fracción de modo que el numerador se convierte en el denominador y el denominador se convierte en el numerador. Por ejemplo, el recíproco de 6/1 es 1/6.
    2. divida la respuesta entre el número de elementos del conjunto.
    3. Tome el recíproco del resultado.

    la media armónica se usa bastante en física. En algunos casos que implican tasas y ratios da un promedio mejor que la media aritmética. También encontrará usos en Geometría, finanzas e Informática.,

  3. media geométrica


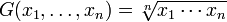
    Este tipo tiene usos muy estrechos y específicos en finanzas, ciencias sociales y tecnología. Por ejemplo, digamos que tienes acciones que ganan 5% el primer año, 20% el segundo año y 10% el tercer año. Si quieres saber la tasa promedio de retorno, no puedes usar el promedio aritmético. ¿Por qué? Porque cuando estás encontrando tasas de retorno estás multiplicando, no sumando. Por ejemplo, el primer año se multiplica por 1.05.,

  4. media aritmética-Geométrica

    esto se usa principalmente en cálculo y en computación de máquinas (es decir, como el básico para muchos cálculos de computadoras). Está relacionado con el perímetro de una elipse. Cuando fue desarrollado por primera vez por Gauss, se utilizó para calcular las órbitas planetarias. La aritmética-geométrica es (no es sorprendente!) una mezcla de las medias aritméticas y geométricas. La matemática es bastante complicada, pero puedes encontrar una explicación relativamente simple de la matemática aquí.,

  5. Root-Mean Square

    es muy útil en campos que estudian las ondas sinusoidales, como la ingeniería eléctrica. Este tipo particular también se llama el promedio cuadrático. Véase: Cuadrática Media / Raíz Media Cuadrada.

  6. Media Heroniana

    utilizada en Geometría para encontrar el volumen de un tronco piramidal. Un tronco piramidal es básicamente una pirámide con la punta cortada.

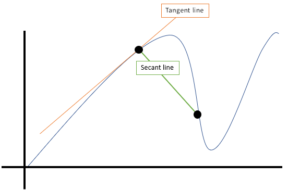
  7. Media gráfica

    otro nombre para la pendiente de la línea secante: el equivalente de la tasa media de cambio entre dos puntos.,

¿Cuál es el modo?

el modo es El número más común en un conjunto. Por ejemplo, el modo en que este conjunto de números es 21:
21, 21, 21, 23, 24, 26, 26, 28, 29, 30, 31, 33

¿Cuál es la Mediana?

la mediana es el número medio en un conjunto de datos. Para encontrar la mediana, enumere sus puntos de datos en orden ascendente y luego encuentre el número medio., El número central en este conjunto es 28, ya que hay 4 números debajo de él y 4 números arriba:
23, 24, 26, 26, 28, 29, 30, 31, 33

cómo encontrar la media, mediana y modo a mano: pasos

cómo encontrar la media, mediana y modo: MODE

cómo encontrar la media, mediana y modo: MEAN

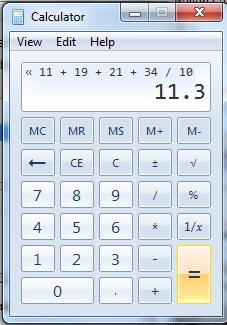
dividiendo la suma por el número de elementos para encontrar la media.

cómo encontrar la media, mediana y modo: mediana

Si tuvo un número impar en el paso 3, Vaya al paso 5. Si tenía un número par, vaya al paso 6.,

Consejo: puede tener más de un modo. Por ejemplo, el modo de 1, 1, 5, 5, 6, 6 es de 1, 5, y 6.

Como la explicación? ¡Echa un vistazo al manual de estadísticas prácticamente engañosas, que tiene cientos de soluciones paso a paso más, al igual que esta!

SPSS mean mode median

para encontrar el SPSS mean mode median, deberá utilizar la pestaña frecuencia. Parece un poco contrario a la intuición, pero la pestaña de Estadísticas descriptivas no le da la opción de encontrar el modo o la mediana.,

SPSS tiene una interfaz muy similar a Microsoft Excel. Por lo tanto, si ha utilizado Microsoft Excel antes, se adaptará rápidamente a SPSS.

SPSS Mean Mode Median: Steps

vea el video o lea los pasos a continuación:

acepte estadísticas, cookies de marketing para ver este video.

pregunta de muestra: encuentre la mediana del modo SPSS para el siguiente conjunto de datos: 20,23,35,66,55,66

Paso 1: Abrir SPSS. En el «¿Qué te gustaría hacer?»cuadro de diálogo, haga clic en el» tipo de Datos «botón de radio y luego haga clic en» OK.»Se abrirá una nueva hoja de trabajo., Nota: Si ha optado por no participar en la primera pantalla de ayuda, es posible que no vea esta opción. En ese caso, comienza en El Paso 2.

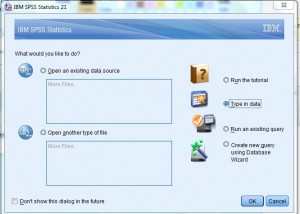
Paso 2: Escriba sus datos en la hoja de trabajo. Puede escribir los datos en una columna o varias columnas si tiene varios conjuntos de datos. Para este ejemplo, escriba 20, 23, 35, 66, 55, 66 en la columna 1. No deje espacios entre los datos (es decir, no deje filas vacías).

Paso 2: Haga clic en «Analizar», pase el cursor sobre» Estadísticas descriptivas «y luego haga clic en «frecuencias».,»

Paso 3: Haga clic en » estadísticas «y luego marque las casillas» Media»,» modo «y» mediana.»Haga clic en» Continuar «dos veces (seleccione» Ninguno » como el tipo de gráfico en la segunda ventana).nota: en algunas versiones de SPSS, es posible que solo tenga que hacer clic en» Continuar » una vez y es posible que no le dé una opción para el tipo de gráfico.

los resultados de frecuencia aparecerán como salida. La parte superior de la salida mostrará la media, el modo y la mediana.

si se desplaza hacia abajo, la tabla de frecuencia también le mostrará el modo., El modo se define en estadísticas como el número con la frecuencia más alta (para este conjunto de datos de muestra, el número que aparece más es 66, con dos resultados en la columna de frecuencia).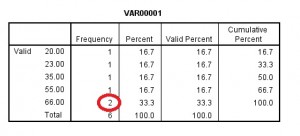

Media, Mediana y modo TI 83

Encontrar la media TI 83 o la mediana TI 83 de una lista de datos se puede lograr de dos maneras: introduciendo una lista de datos o utilizando la pantalla de inicio para escribir los comandos., Usar la función de lista es tan fácil como ingresar los datos en la pantalla de inicio, y tiene la ventaja adicional de que puede usar los datos para otros fines después de haber calculado su media, modo y mediana (por ejemplo, es posible que desee crear un histograma TI 83).

pasos para la media, la mediana y el modo en el TI 83

vea el video para la media y la mediana o lea los pasos debajo (para el modo, consulte esta nota):

acepte estadísticas, cookies de marketing para ver este video.

Paso 1: Ingrese los datos anteriores en una lista., Presione el botón STAT y luego presione ENTER. Introduzca el primer número (1250) y, a continuación, pulse Intro. Continúe ingresando números, presionando el botón ENTER después de cada entrada.

Paso 2: Pulse el botón STAT.

Paso 3: Presione el botón de flecha derecha para resaltar » Calc.»

Paso 4: Presione ENTER para elegir «1-Var Stats» y luego escriba el nombre de la lista. Por ejemplo, para introducir L1 pulse y .

Paso 5: Presione ENTER de nuevo. La calculadora devolverá la media, x. Para esta lista de datos, la media TI 83 es 884.05 pies (redondeada a 3 decimales).

Paso 6: flecha hacia abajo hasta que vea » Med.,»Esta es la mediana TI 83; para los datos anteriores, la mediana es de 813.05 pies.

Nota: El TI-83 plus no tiene una función de modo incorporada, pero una vez que haya ingresado a su lista, es bastante fácil detectar el modo: es solo el número que ocurre más a menudo en el conjunto. ¿No estás seguro? Lea más sobre el modo aquí.

Eso es todo!

¿perdiste tu guía? Descargue uno nuevo aquí en el sitio web de TI.

——————————————————————————

Necesito ayuda con una tarea o cuestión de prueba?, Con Chegg Study, puede obtener soluciones paso a paso a sus preguntas de un experto en el campo. ¡Tus primeros 30 minutos con un tutor de Chegg son GRATIS!