Men. Siento, de alguna manera, que me gusta lo que estás diciendo.Soc. Y a mí, Meno, me gusta lo que estoy diciendo.
del Meno de Platón
La longitud de la diagonal del cuadrado unitario es igual a la raíz cuadrada de 2.
la longitud de la diagonal de la unidad cuadrada es igual a √2. Bueno, esto no es realmente una gran noticia. Cada uno que alguna vez se encontró con el teorema de Pitágoras es consciente del hecho., En el triángulo rectángulo isósceles con las piernas de longitud 1, la hipotenusa, de acuerdo con el teorema de Pitágoras – 12 + 12 = (hipotenusa)2 – es de hecho de longitud √2. La motivación de esta página no es tanto ese hecho en sí, sino la forma de mostrarlo sin recurrir al famoso teorema. De hecho, se podría argumentar que el teorema de Pitágoras podría haber sido utilizado en exceso, ver un curioso ejemplo.
Un argumento que se remonta a la figura dibujada por Sócrates en el Meno de Platón podría haber sido conocido por el propio Pitágoras, aunque este último vivió un siglo antes.,
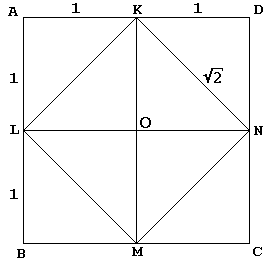
en el diálogo, Sócrates, a su manera habitual, conduce a un joven esclavo a una construcción de un cuadrado dos veces el área del dado:
el cuadrado dado KLMN con centro O se corta primero por sus diagonales en 4 triángulos iguales. Sócrates incrusta KLMN en un cuadrado más grande ABCD como si reflejara estos triángulos cada uno en su hipotenusa. El esclavo entonces admite – ¿y quién no? – ese cuadrado ABCD es dos veces más grande que el cuadrado KLMN.
La verdad sea dicha, el cuadrado ABCD de Sócrates midió 4 en el lado, tal que el cuadrado KLMN tenía área de 8., Está claro que cuando comenzamos con el cuadrado ABCD del lado 2 (y por lo tanto del área 4), El cuadrado KLMN tendrá área de 2.
ahora, en general, para un número positivo A, √A se define como un número cuyo cuadrado es A:
(√a) 2.
por otro lado, cada estudiante de áreas sabe, que el área de un cuadrado de lado B es igual a b2. Se deduce entonces que el lado de un cuadrado con área a es exactamente √A. concluimos que el lado del cuadrado KLMN es igual a √2. Por un lado,
KN = √A.
el punto central del argumento es el hecho de que, en el diagrama, KN juega un doble papel., Además de ser uno de los lados del cuadrado KLMN, también sirve como diagonal del cuadrado OKDN. Este último es, por supuesto, una unidad cuadrada, lo que demuestra nuestra afirmación.
(desde una perspectiva un poco diferente el mismo episodio se menciona en otra parte.)
















Deja una respuesta