Cuando los Ángulos de un Triángulo no suman 180 Grados

1. Introducción

¿los ángulos de un triángulo suman 180 grados o $\pi$ radianes? La respuesta es «a veces sí, a veces no». Es esta una pregunta importante? Sí, porque nos lleva a entender que hay diferentes geometrías basadas en diferentes axiomas o’reglas del juego de la geometría’. ¿Es una pregunta significativa? Bueno, no, al menos no hasta que hayamos acordado el significado de las palabras «ángulo» y «triángulo», no hasta que sepamos las reglas del juego., En este artículo discutimos brevemente los axiomas subyacentes y damos una prueba simple de que la suma de los ángulos de un triángulo en la superficie de una esfera unitaria no es igual a $\pi.sino a$ \pi plus más el área del triángulo. Usaremos el hecho de que el área de la superficie de una esfera unitaria es 4 4\pi pi.

2. El Gran Teorema

antes de que podamos decir lo que es un triángulo necesitamos ponernos de acuerdo sobre lo que queremos decir con puntos y rectas. Estamos trabajando en geometría esférica (literalmente geometría en la superficie de una esfera)., En esta geometría el espacio es la superficie de la esfera; los puntos son puntos en esa superficie, y la línea de la distancia más corta entre dos puntos es el gran círculo que contiene los dos puntos. Un gran círculo (como el Ecuador) corta la esfera en dos hemisferios iguales. Esta geometría tiene aplicaciones obvias a distancias entre lugares y rutas aéreas en la Tierra.,

esfera giratoria que muestra un gran círculo

el ángulo entre dos grandes círculos en un punto P es el ángulo euclidiano entre las direcciones de los círculos (o estrictamente entre las tangentes a los círculos en P). Esto no presenta ninguna dificultad en la navegación en la Tierra porque en cualquier punto dado pensamos en el ángulo entre dos direcciones como si la Tierra fuera plana en ese punto.

un lune es una parte de la superficie de la esfera delimitada por dos grandes círculos que se encuentran en puntos antípodas., Primero consideramos el área de un lune y luego introducimos otro gran círculo que divide el lune en triángulos.

Rotación de la esfera mostrando 4 lunes

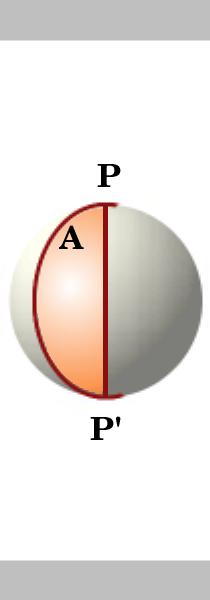
Lema.

el área de un lune en un círculo de radio unitario es el doble de su ángulo, es decir, si el ángulo del lune es A, entonces su área es 2A. dos grandes círculos que se cruzan en los puntos antipodales P Y P’ dividen la esfera en 4 lunes. El área de la superficie de una esfera unitaria es 4 4 \ pi pi.,

Las áreas de los lunes son proporcionales a sus ángulos en P de manera que el área de un lune con ángulo a es

${\frac{A}{2\pi}\times {4\pi}= {2A}}$

el Ejercicio 1.

¿Cuáles son las áreas de los otros 3 lunes? ¿Sus 4 áreas suman $4 \ pi??

Compruebe sus respuestas aquí .

los lados de un triángulo ABC son segmentos de tres grandes círculos que en realidad cortan la superficie de la esfera en ocho triángulos esféricos. Entre los dos grandes círculos a través del punto a Hay cuatro ángulos., Etiquetamos el ángulo dentro del triángulo ABC como ángulo A, y de manera similar los otros ángulos del triángulo ABC como ángulo B y ángulo C.

esfera giratoria que muestra 8 triángulos

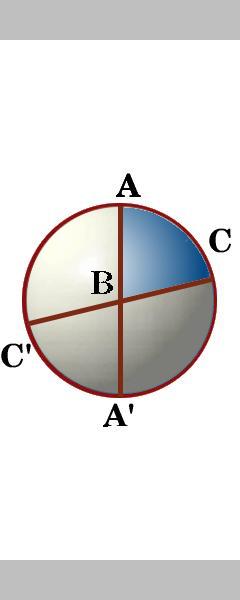
Ejercicio 2

girando la esfera ¿puede nombrar los ocho triángulos y decir si alguno de ellos tiene la misma área? Revisa tus respuestas aquí .

Teorema.

considere un triángulo esférico ABC en la esfera unitaria con ángulos A, B y C. Entonces el área del triángulo ABC es

A + B + C – \ \ pi..,

el diagrama muestra una vista mirando hacia abajo en el hemisferio que tiene la línea a través de AC como su límite. Las regiones marcadas como Área 1 y área 3 son lunes con ángulos A y C respectivamente. Considere los lunes a través de B y B’. El triángulo ABC es congruente con el triángulo A’B’C’ Por lo que el área sombreada en forma de pajarita, marcada Área 2, que es la suma de las áreas de los triángulos ABC y A’BC’, es igual a la zona del lune con ángulo B, que es igual a 2B.,

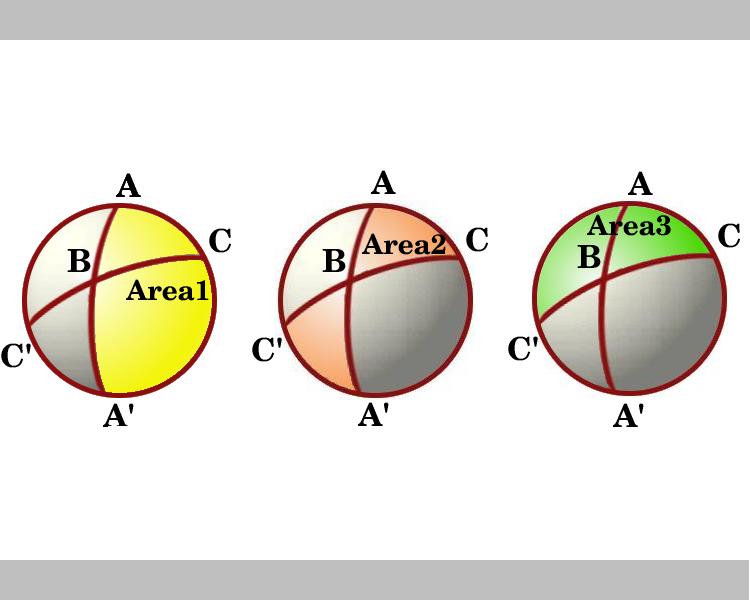
así que en el diagrama vemos las áreas de tres lunes y, usando el lema, estas son:

Área 1 = 2a
Área 2 = 2b
Área 3 = 2C

al sumar estas tres áreas incluimos el área del triángulo ABC tres veces., Hence

3., Geometría no euclidiana

a veces los descubrimientos revolucionarios no son más que ver realmente lo que ha estado bajo nuestras narices todo el tiempo. Este fue el caso sobre el descubrimiento de la geometría no euclidiana en el siglo XIX. Durante unos 2000 años después de Euclides escribió sus «elementos» en 325 antes de Cristo la gente trató de probar el postulado paralelo como un teorema en la geometría de los otros axiomas, pero siempre fracasó y thatis una larga historia., Mientras tanto, los matemáticos usaban geometría esférica todo el tiempo, una geometría que obedece a los otros axiomas de la geometría euclidiana y contiene muchos de los mismos teoremas, pero en la que el postulado paralelo no se sostiene. Todo el tiempo tenían un ejemplo de una geometría no euclidiana bajo sus narices.

piense en una línea L y un punto P no en L. La gran pregunta es: «¿Cuántas líneas se pueden dibujar a través de P paralelas a L?»En geometría euclidiana la respuesta es» exactamente uno » y esta es una versión del postulado paralelo., Si la suma de los ángulos de cada triángulo en la geometría es radi\pi radi radianes, entonces el postulado paralelo se mantiene y viceversa, las dos propiedades son equivalentes.

en geometría esférica, los axiomas básicos que asumimos (las reglas del juego) son diferentes de la geometría euclidiana, esta es una geometría no euclidiana. Hemos visto que en geometría esférica los ángulos de los triángulos no siempre suman radi \ pi radi radianes por lo que no esperaríamos que el postulado paralelo se mantenga., En geometría esférica, las líneas rectas (líneas de distancia más corta o geodésicas)son grandes círculos y cada línea en la geometría corta cada otra línea en dos puntos. La respuesta a la gran pregunta sobre los paralelos es`si tenemos una línea L y un punto P no en L, entonces no hay líneas a través de P paralelas a la línea L.,»

Los matemáticos griegos (por ejemplo Ptolomeo C 150) calcularon las mediciones de triángulos esféricos en ángulo recto y trabajaron con fórmulas de trigonometría esférica y los matemáticos árabes (por ejemplo Jabir ibn Aflah C 1125 y Nasir ed-din c 1250) extendieron el trabajo aún más. La fórmula discutida en este artículo fue descubierta por Harriot en 1603 y publicada por Girard en 1629. Otras ideas del tema fueron desarrolladas por Saccerhi (1667-1733).,

Todo esto fue en gran medida inadvertido por los descubridores del siglo XIX de la geometría hiperbólica, que es otra geometría no euclidiana donde el postulado paralelo no se sostiene. En la geometría esférica (también llamada geometría elíptica) los ángulos de los triángulos suman más de $\pi$ radianes y en la geometría hiperbólica de los ángulos de los triángulos suman menos de $\pi$ radianes.

para más información ver el artículo de Alan Beardon ‘ ¿cuántas geometrías hay?’y el artículo de Keith Carne ‘geometrías extrañas’., Hay algunas actividades prácticas que puedes probar para explorar estas geometrías en http://nrich.maths.org/MOTIVATE/conf8/index.html