Mostrar Aviso móvil Mostrar todas las notas ocultar todas las notas
sección 3-1 : ecuaciones y curvas paramétricas
Hasta este punto (tanto en Cálculo I como en Cálculo II) hemos mirado casi exclusivamente las funciones en la forma \(y = f\left( x \right)\) O \(x = h\left( y \right)\) y casi todas las fórmulas que hemos desarrollado requieren que las funciones estén en una de estas dos formas. El problema es que no todas las curvas o ecuaciones que nos gustaría ver caen fácilmente en esta forma.
Tome, por ejemplo, un círculo. Es bastante fácil escribir la ecuación de un círculo centrado en el origen con Radio \(r\).,
\
sin embargo, nunca podremos escribir la ecuación de un círculo como una sola ecuación en cualquiera de las formas anteriores. Claro que podemos resolver para \(x\) O \(y\) como las siguientes dos fórmulas muestran
\
pero de hecho hay dos funciones en cada una de ellas. Cada fórmula da una porción del círculo.
\
desafortunadamente, normalmente estamos trabajando en todo el círculo, o simplemente no podemos decir que vamos a estar trabajando solo en una parte de él. Incluso si podemos reducir las cosas a solo una de estas porciones, la función sigue siendo a menudo bastante desagradable para trabajar.,
\
esta tercera variable generalmente se denota por \(t\) (como hicimos aquí), pero no tiene que ser, por supuesto. A veces restringiremos los valores de \(t\) que usaremos y otras veces no. esto a menudo dependerá del problema y de lo que estemos intentando hacer.
para ayudar a visualizar lo que una curva paramétrica es pretender que tenemos un gran tanque de agua que está en constante movimiento y dejamos caer una pelota de ping pong en el tanque., El punto \(\left( {x,y} \right) = \left( {f\left( t \right),g\left( t \right)} \right)\) entonces representar la ubicación de la pelota de ping pong en el tanque en el tiempo \(t\) y la curva paramétrica será un rastro de todos los lugares de la pelota de ping pong. Tenga en cuenta que esto no siempre es una analogía correcta, pero es útil inicialmente para ayudar a visualizar lo que es una curva paramétrica.
dibujar una curva paramétrica no siempre es algo fácil de hacer. Echemos un vistazo a un ejemplo para ver una forma de dibujar una curva paramétrica., Este ejemplo también ilustrará por qué este método no suele ser el mejor.
en este punto nuestra única opción para dibujar una curva paramétrica es elegir valores de \(t\), conectarlos a las ecuaciones paramétricas y luego trazar los puntos. Por lo tanto, vamos a conectar algunos \(t\)’s.,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Desafortunadamente, no hay una respuesta real a esta pregunta en este momento. Simplemente elegimos \(t\) ‘ s hasta que estamos bastante seguros de que tenemos una buena idea de cómo se ve la curva. Es este problema con la selección de valores» buenos » de \(t\) lo que hace que este método de dibujar curvas paramétricas sea una de las opciones más pobres. A veces no tenemos opción, pero si tenemos opción deberíamos evitarla.
discutiremos un método gráfico alternativo en ejemplos posteriores que ayudará a explicar cómo se eligieron estos valores de \(t\).,
tenemos una idea más que discutir antes de dibujar la curva. Las curvas paramétricas tienen una dirección de movimiento. La dirección del movimiento viene dada por el aumento de \(t\). Por lo tanto, al trazar curvas paramétricas, también incluimos flechas que muestran la dirección del movimiento. A menudo daremos el valor de \(t\) que dio puntos específicos en el gráfico, así como para dejar claro el valor de \(t\) que dio ese punto en particular.
Aquí está el bosquejo de esta curva paramétrica.
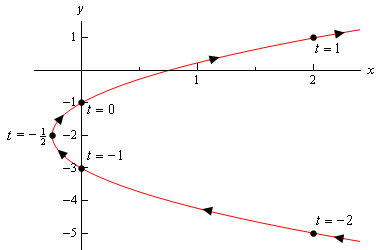
Así, parece que tenemos una parábola que se abre hacia la derecha.,
antes de terminar este ejemplo hay un punto algo importante y sutil que necesitamos discutir primero. Observe que nos aseguramos de incluir una porción del croquis a la derecha de los puntos correspondientes a \(t = – 2\) y \(t = 1\) para indicar que hay porciones del croquis allí. Si simplemente hubiéramos detenido el boceto en esos puntos, estamos indicando que no había ninguna porción de la curva a la derecha de esos puntos y claramente lo habrá. Simplemente no calculamos ninguno de esos puntos.,
esto puede parecer un punto sin importancia, pero como veremos en el siguiente ejemplo es más importante de lo que podríamos pensar.
Antes de abordar de una manera mucho más fácil esbozar este gráfico primero vamos a abordar la cuestión de límites en el parámetro. En el ejemplo anterior no teníamos ningún límite en el parámetro. Sin límites en el parámetro, el gráfico continuará en ambas direcciones como se muestra en el CROQUIS anterior.
sin embargo, a menudo tendremos límites en el parámetro y esto afectará el croquis de las ecuaciones paramétricas., Para ver este efecto, veamos una ligera variación del ejemplo anterior.
tenga en cuenta que la única diferencia aquí es la presencia de los límites en \(t\). Todos estos límites nos dicen que no podemos tomar ningún valor de \(t\) fuera de este rango. Por lo tanto, la curva paramétrica solo será una porción de la curva anterior. Aquí está la curva paramétrica para este ejemplo.,
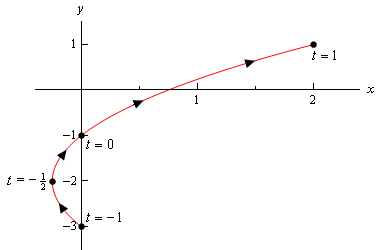
observe que con este croquis iniciamos y detenemos el CROQUIS directamente en los puntos que se originan en los puntos finales del rango de \(t\)’s. contrasta esto con el croquis en el ejemplo anterior donde teníamos una porción del croquis a la derecha de los puntos» inicio «y» fin » que calculamos.
en este caso la curva comienza en \(t = – 1\) y termina en \(t = 1\), mientras que en el ejemplo anterior la curva realmente no comenzó en la mayoría de los puntos correctos que calculamos., Necesitamos ser claros en nuestros bocetos si la curva comienza/termina justo en un punto, o si ese punto fue simplemente el primero/último que calculamos.
ahora es el momento de echar un vistazo a un método más fácil de dibujar esta curva paramétrica. Este método utiliza el hecho de que en muchos casos, pero no en todos, podemos eliminar el parámetro de las ecuaciones paramétricas y obtener una función que solo involucre \(x\) y \(y\). A veces llamaremos a esto la ecuación algebraica para diferenciarla de las ecuaciones paramétricas originales., Habrá dos pequeños problemas con este método, pero será fácil abordar esos problemas. Sin embargo, es importante tener en cuenta que no siempre podremos hacer esto.
la forma en que eliminemos el parámetro dependerá de las ecuaciones paramétricas que tengamos. Vamos a ver cómo eliminar el parámetro para el conjunto de ecuaciones paramétricas que hemos estado trabajando con hasta este punto.
obtener un boceto de la curva paramétrica una vez que hemos eliminado el parámetro parece bastante simple. Todo lo que necesitamos hacer es graficar la ecuación que encontramos eliminando el parámetro., Sin embargo, como ya se señaló, Hay dos pequeños problemas con este método. La primera es la dirección del movimiento. La ecuación que implica solamente \(x\) y \(y\) no dará la dirección del movimiento de la curva paramétrica. Sin embargo, esto es generalmente un problema fácil de solucionar. Echemos un vistazo rápido a las derivadas de las ecuaciones paramétricas del último ejemplo. Son,
\
tenga en cuenta que la derivada \(x\) no es tan útil para este análisis, ya que será tanto positiva como negativa y, por lo tanto, \(x\) aumentará y disminuirá dependiendo del valor de \(t\)., Eso no ayuda mucho con la dirección, ya que seguir la curva en cualquier dirección mostrará tanto el aumento como la disminución \(x\).
en algunos casos, solo una de las ecuaciones, como este ejemplo, dará la dirección, mientras que en otros casos cualquiera de las dos podría ser utilizado. También es posible que, en algunos casos, ambos derivados sean necesarios para determinar la dirección. Siempre dependerá del conjunto individual de ecuaciones paramétricas.,
el segundo problema con la eliminación del parámetro se ilustra mejor en un ejemplo, ya que nos encontraremos con este problema en los ejemplos restantes.
bien, ese fue un ejemplo muy largo. La mayoría de estos tipos de problemas no son tan largos. Teníamos mucho que discutir en este caso para poder sacar un par de ideas importantes del camino. El resto de los ejemplos en esta sección no debería tardar tanto en pasar.
ahora, echemos un vistazo a otro ejemplo que ilustrará una idea importante sobre las ecuaciones paramétricas.,
por lo tanto, vimos en los dos últimos ejemplos dos conjuntos de ecuaciones paramétricas que de alguna manera dieron el mismo gráfico. Sin embargo, debido a que trazaron el gráfico un número diferente de veces realmente necesitamos pensar en ellas como diferentes curvas paramétricas al menos de alguna manera. Esto puede parecer una diferencia de la que no tenemos que preocuparnos, pero como veremos en secciones posteriores, esta puede ser una diferencia muy importante. En algunas de las secciones posteriores vamos a necesitar una curva que se traza exactamente una vez.,
antes de pasar a otros problemas vamos a reconocer brevemente lo que sucede al cambiar la \(t\) A UN nt en este tipo de ecuaciones paramétricas. Cuando estamos tratando con ecuaciones paramétricas que involucran solo senos y cosenos y ambos tienen el mismo argumento si cambiamos el argumento de \(t\) A nt simplemente cambiamos la velocidad con la que se traza la curva. If \(N> 1\) aumentaremos la velocidad y if \(N< 1\) disminuiremos la velocidad.
echemos un vistazo a un par de ejemplos más.,
hasta este punto hemos visto ejemplos que trazarían el gráfico completo que obtuvimos eliminando el parámetro si tomamos un rango lo suficientemente grande de \(t\)’s. Sin embargo, en el ejemplo anterior ahora hemos visto que este no siempre será el caso. Es más que posible tener un conjunto de ecuaciones paramétricas que continuamente trazar sólo una porción de la curva. Por lo general, podemos determinar si esto sucederá buscando límites en \(x\) y \(y\) que se nos imponen por la ecuación paramétrica.,
a menudo usaremos ecuaciones paramétricas para describir la ruta de un objeto o partícula. Echemos un vistazo a un ejemplo de eso.
debemos dar una pequeña advertencia en este punto. Debido a las ideas involucradas en ellas, nos concentramos en curvas paramétricas que rastreaban porciones de la curva más de una vez. Sin embargo, no se encierren demasiado en la idea de que esto siempre sucederá. Muchas, si no la mayoría de las curvas paramétricas solo se trazarán una vez. El primero que vimos es un buen ejemplo de esto. Esa curva paramétrica nunca repetirá ninguna porción de sí misma.,
hay un último tema que se discutirá en esta sección antes de Continuar. Hasta ahora hemos comenzado con ecuaciones paramétricas y eliminado el parámetro para determinar la curva paramétrica.
sin embargo, hay momentos en los que queremos ir por el otro lado. Dada una función o ecuación es posible que desee escribir un conjunto de ecuaciones paramétricas para ella. En estos casos decimos que parametrizamos la función.
si tomamos los ejemplos 4 y 5 como ejemplos podemos hacer esto para elipses (y por lo tanto círculos)., Dada la elipse
\
un conjunto de ecuaciones paramétricas para ello sería,
\
Este conjunto de ecuaciones paramétricas trazará la elipse comenzando en el punto \(\left( {a, 0} \right)\) y trazará en sentido contrario a las agujas del reloj y trazará exactamente una vez en el rango \(0 \Le t \Le 2\pi \). Este es un conjunto bastante importante de ecuaciones paramétricas, ya que se utiliza continuamente en algunos temas con el trato con elipses y/o círculos.
cada curva se puede parametrizar de más de una manera. Cualquiera de los siguientes parámetros también parametrizará la misma elipse.,
\
la presencia de la \(\omega \) cambiará la velocidad a la que gira la elipse como vimos en el Ejemplo 5. Tenga en cuenta también que los dos últimos trazarán elipses con una dirección de movimiento en el sentido de las agujas del reloj (es posible que desee verificar esto). También tenga en cuenta que no todos empezamos en el mismo lugar (si pensamos en \(t = 0\) como el punto de partida que es).
Hay muchas más parametrizaciones de una elipse, por supuesto, pero entiendes la idea. Es importante recordar que cada parametrización trazará la curva una vez con un rango potencialmente diferente de \(t\) ‘ s., Cada parametrización puede girar con diferentes direcciones de movimiento y puede comenzar en diferentes puntos.
Puede encontrar que necesita una parametrización de una elipse que comienza en un lugar particular y tiene una dirección particular de movimiento y así ahora sabe que con un poco de trabajo puede escribir un conjunto de ecuaciones paramétricas que le darán el comportamiento que está buscando.
Ahora, vamos a escribir un par de otras parametrizaciones importantes y todos los comentarios sobre la dirección del movimiento, el punto de partida y el rango de \(t\)’S para un trazo (si corresponde) siguen siendo verdaderos.,
primero, porque un círculo no es más que un caso especial de una elipse podemos usar la parametrización de una elipse para obtener las ecuaciones paramétricas para un círculo centrado en el origen de radius \(r\) también. Una forma posible de parametrizar un círculo es,
\ \
en este punto puede no parecer tan útil hacer una parametrización de una función como esta, pero hay muchos casos en los que en realidad será más fácil, o incluso puede ser necesario, trabajar con la parametrización en lugar de la función en sí., Desafortunadamente, casi todos estos casos ocurren en un curso de cálculo III.
















Deja una respuesta