Mostrar Aviso móvil Mostrar todas las notas ocultar todas las notas
sección 4-11 : aproximaciones lineales
en esta sección vamos a echar un vistazo a una aplicación no de derivadas sino de la recta tangente a una función. Por supuesto, para obtener la línea tangente necesitamos tomar derivados, así que de alguna manera esto es una aplicación de derivados también.
\
eche un vistazo al siguiente gráfico de una función y su línea tangente.
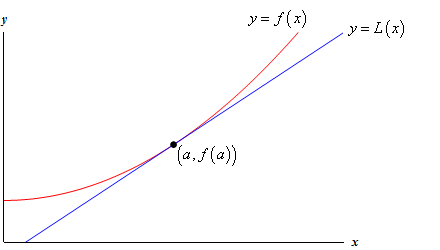
Así que, ¿por qué hacemos esto? Echemos un vistazo a un ejemplo.,
las aproximaciones lineales hacen un muy buen trabajo aproximando valores de \(f\left( x \right)\) siempre y cuando permanezcamos «cerca» de \(x = a\). Sin embargo, cuanto más lejos de \(x = a\) obtengamos, peor será la aproximación. El problema principal aquí es que lo cerca que necesitamos permanecer a \(x = A\) para obtener una buena aproximación dependerá tanto de la función que estamos usando como del valor de \(x = a\) que estamos usando. Además, a menudo no habrá una manera fácil de predecir cuán lejos de \(x = A\) podemos llegar y aún así tener una aproximación «buena».,
echemos un vistazo a otro ejemplo que en realidad se usa bastante en algunos lugares.
esto es en realidad una aproximación lineal algo importante. En óptica, esta aproximación lineal se utiliza a menudo para simplificar las fórmulas. Esta aproximación lineal también se utiliza para ayudar a describir el movimiento de un péndulo y las vibraciones en una cuerda.
















Deja una respuesta