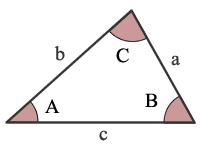
figura triangular ángulo-ángulo lateral (ASA)
A = ángulo a
B = ángulo b
C = ángulo C
a = lado a
b = lado b
c = Lado c
P = perímetro
s = semi-perímetro
K = área
R = Radio del círculo inscrito
R = Radio del círculo circunscrito
Calculator Use
cada opción de cálculo, que se muestra a continuación, tiene sub-viñetas que enumeran la secuencia de métodos utilizados en esta calculadora para resolver los valores de ángulo y lado desconocidos, incluida la suma de ángulos en un triángulo, la ley de senos y la ley de cosenos., Estas no son las únicas secuencias que podría utilizar para resolver este tipo de problemas.
- vea también estas calculadoras de trigonometría:
- Calculadora de la Ley de cosenos
- Calculadora de la Ley de senos
teoremas de triángulo de solución
especificar los tres ángulos de un triángulo no identifica de manera única un triángulo. Por lo tanto, especificar dos ángulos de un tringle le permite calcular solo el tercer ángulo.,
dado el tamaño de 2 ángulos de un triángulo se puede calcular el tamaño del tercer ángulo. El total será igual a 180 ° o π radianes.
C = 180° – A – B (en grados)
C = π – A – B (en radianes)
AAS es Ángulo, Ángulo, lado
dado el tamaño de 2 ángulos y 1 lado opuesto a uno de los ángulos dados, puede calcular los tamaños de los restantes 1 ángulo y 2 lados.
use la regla de la suma de ángulos para encontrar el otro ángulo, luego
use la Ley de senos para resolver para cada uno de los otros dos lados.,
ASA es Ángulo, lado, ángulo
dado el tamaño de 2 ángulos y el tamaño del lado que está entre esos 2 ángulos, puede calcular los tamaños del 1 ángulo restante y los 2 lados.
use la regla de la suma de ángulos para encontrar el otro ángulo, luego
use la Ley de senos para resolver para cada uno de los otros dos lados.,
ASS (o SSA) es Ángulo, Lado, Lado
dado el tamaño de 2 lados (a y c donde a < c) y el tamaño del ángulo a que no está entre esos 2 lados, es posible que pueda calcular los tamaños de los restantes 1 lado y 2 ángulos, dependiendo de las siguientes condiciones.,F cosenos para resolver para cada uno de los otros dos ángulos
presente 2 soluciones completas
Ejemplo: 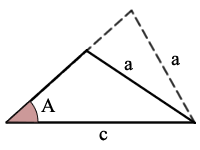
sin(A) = A/c, hay un triángulo posible
use la Ley de senos para resolver para un ángulo, C
use la regla de suma de ángulos para encontrar el otro ángulo, b
Use la Ley de Sines para resolver para el último lado, b
Ejemplo: 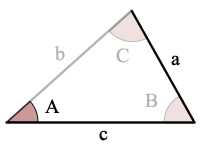
sin(a) > A/C, no hay triángulos posibles
aviso de error: sin(a) > A/C Por lo que no hay soluciones y ningún triángulo!,
Ejemplo: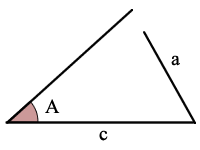
SAS es Side, Angle, Side
dado el tamaño de 2 lados (c y a) y el tamaño del ángulo B que está entre esos 2 lados, puede calcular los tamaños de los restantes 1 lado y 2 ángulos.
use la Ley de cosenos para resolver para el lado restante, b
determine qué lado, a O c, es más pequeño y use la Ley de senos para resolver para el tamaño del ángulo opuesto, a O C respectivamente.,
use la regla de la suma de ángulos para encontrar el último ángulo
SSS es Side, Side, Side
dado el tamaño de los 3 lados, puede calcular el tamaño de los 3 ángulos en el triángulo.
use la Ley de cosenos para resolver los ángulos. También puede usar la regla de la suma de ángulos para encontrar el ángulo final una vez que conozca 2 de ellos.,sin-1
Ley de cosenos
Si a, b y c son las longitudes de las piernas de un triángulo opuesto a los ángulos A, B y C respectivamente; entonces la Ley de cosenos establece:
A2 = c2 + B2 – 2BC cos a, resolviendo para cos a, cos a = ( b2 + c2 – a2 ) / 2BC
b2 = A2 + c2 – 2CA cos B, resolviendo para cos B, cos B = ( c2 + a2 – b2 ) / 2CA
C2 = B2 + A2 – 2AB Cos C, solving for Cos C, Cos C = ( a2 + b2 – c2 ) / 2ab
solving, for example, for an angle, a = cos-1
other Triangle characteristics
Triangle Perimeter, p = a + b + c
triangle semi-Perimeter, s = 0.,5 * (a + b + c)
Área del triángulo, k = √
radio del círculo inscrito en el triángulo, r = √
radio del círculo circunscrito alrededor del triángulo, R = (abc) / (4K)
referencias/ lectura adicional
Weisstein, Eric W. «Ass Theorem.»From MathWorld A A Wolfram Web Resource. Teorema del culo.
Las matemáticas son triángulos SAS que resuelven la diversión
















Deja una respuesta