Los vectores son ampliamente útiles en la ciencia para describir cualquier cosa que tenga tanto una dirección como una magnitud. Por lo general, se dibujan con la ayuda de flechas puntiagudas, cuya longitud representará la magnitud del vector. Un pase de mariscal de campo es el ejemplo simple porque tiene la dirección generalmente en algún lugar downfield y una magnitud. A veces tenemos que manejar dos vectores juntos trabajando en algún objeto. En tales casos los ángulos entre esos vectores son importantes., Este tema explicará el ángulo entre dos vectores fórmula, así como ejemplos. ¡Vamos a aprenderlo!
concepto de vectores
fuera del campo, los vectores se pueden utilizar para representar cualquier número de objetos físicos o actividades. Por ejemplo. El viento, por ejemplo, es una cantidad vectorial. Es porque en cualquier lugar dado tiene una dirección así como la magnitud. Podemos hacer un mapa del flujo de aire en cualquier momento, entonces, dibujando los vectores de viento para un número de diferentes ubicaciones geográficas.
muchas propiedades de objetos en movimiento también son vectores., En la bola de billar, su vector de velocidad describe su movimiento. Muestra la dirección de las marcas de flecha del vector como la dirección del movimiento, y la longitud del vector representa la velocidad de la bola.
el impulso de la bola de billar es también un ejemplo de cantidad vectorial. Como es igual a masa veces velocidad. Por lo tanto, el vector de momento de los puntos de bola en la misma dirección que su vector de velocidad. Y la magnitud del vector de momento será el producto de la multiplicación de la velocidad de la bola y su masa.,
en términos matemáticos, un vector es cualquier objeto que tiene una magnitud y dirección definibles. Como los vectores no son lo mismo que las líneas o formas estándar, necesitamos usar algunas fórmulas especiales para encontrar ángulos entre ellos.
la fórmula para el ángulo entre dos vectores
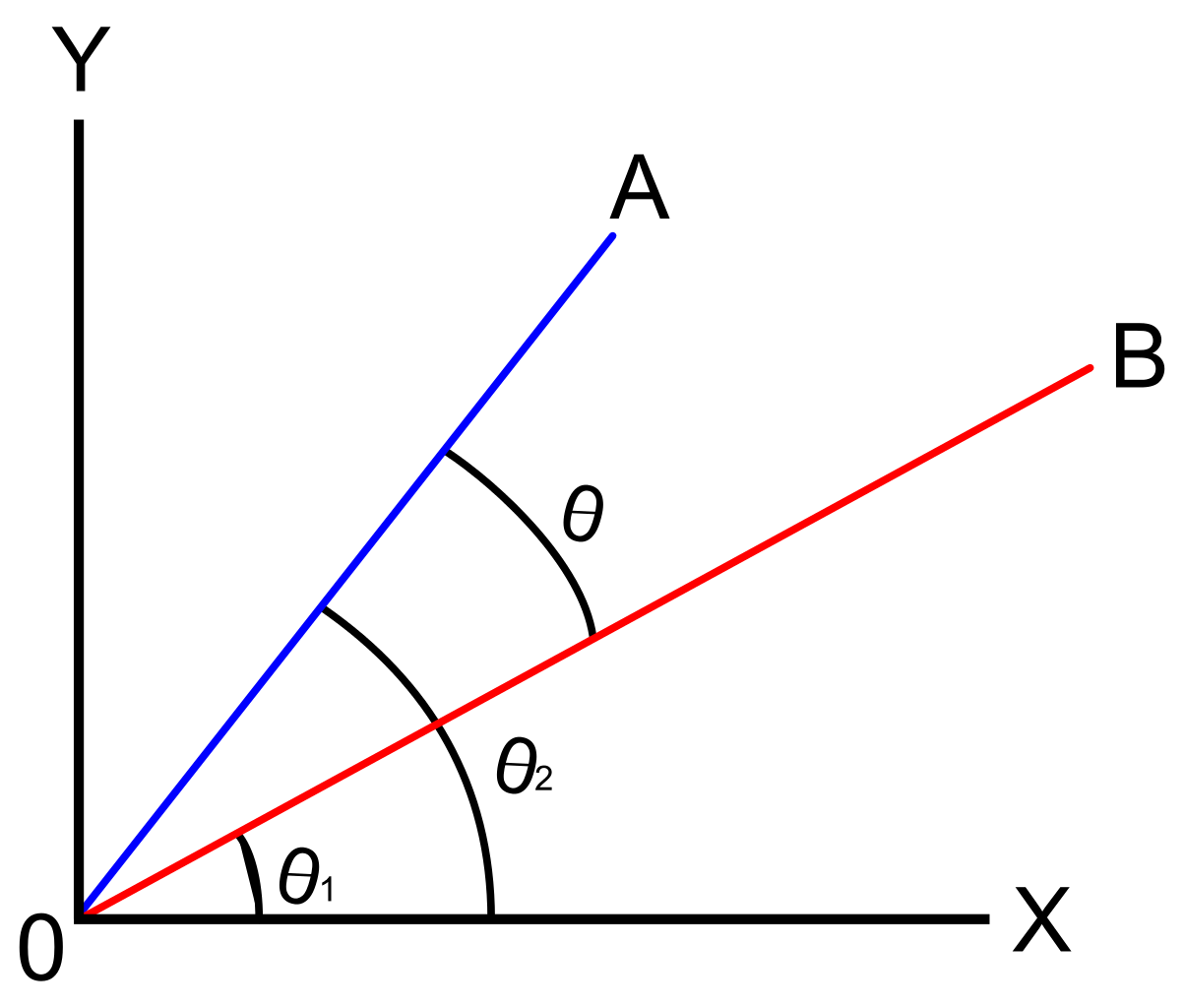
El ángulo entre dos vectores será diferido por un solo punto, que se llama como el ángulo más corto en el que tenemos que girar alrededor de uno de los vectores a la posición de co-direccional con otro vector.,
la discusión sobre los ángulos de dirección de los vectores se centra en encontrar el ángulo de un vector con respecto al eje X positivo. Esto se centrará en el ángulo entre dos vectores en la posición estándar. Se dice que un vector está en posición estándar si su punto inicial es el origen (0, 0).
si los dos vectores se asumen como a y b, entonces el punto creado se define como a .B. supongamos que estos dos vectores están separados por el ángulo \(\theta\). Para saber cuál es la medida del ángulo vamos a resolver con la ayuda de la fórmula dada:
conocemos el producto escalar:
\(\vec{a}.,\vec{b} =|\vec{a}||\vec{b}|cos\theta\)
Ahora, el ángulo entre dos vectores fórmula es:
\(\theta = cos^{-1}\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}\)
Donde \\(theta\) es el ángulo entre a y b vectores.
Resuelto Ejemplos para el Ángulo entre Dos Vectores Fórmula
P. 1: Calcular el ángulo entre dos vectores 3i + 4j – k y 2i – j + k.
Solución: Vamos,
a = 3i + 4j – k y
b = 2i – j + k
se define el producto escalar como:
un .b = (3i + 4j-k).(2i – j + k)
















Deja una respuesta